1.) в арифметической прогрессии 11 членов. первый, пятый и одиннадцатый члены составляют прогрессию. найти сумму всех одиннадцати членов данной арифметической прогрессии, если первый член равен 24 и разность отлична от нуля. 2.) x^2+корень из (x^2-3x+5) > 7+3x
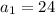

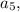
 образуют геометрическую прогрессию, то
образуют геометрическую прогрессию, то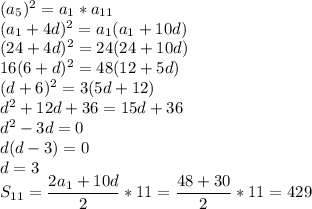
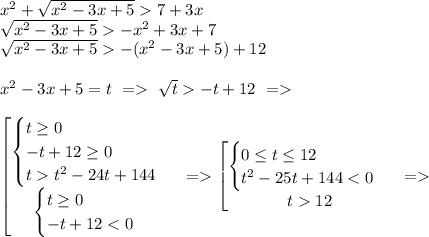
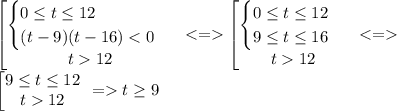

![(-\infty;-1] \cup [4; +\infty)](/tpl/images/0173/2580/46497.png)



a1,a5,a11 -b1,b2,b3 соответственно ,
a1=24
{24=24
{b1q=a1+4d
{b1q^2=a1+10d
{24q=24+4d
{24q^2=24+10d
d=(24q-24)/4
24q^2=24+10((24q-24)/4)
решая получаем q=1(не подходит), q=3/2
значит разность d=3
S11=(2*24+10*3)/2*11=429 ответ 429
2)
x^2+√x^2-3x+5 >7+3x
ОДЗ
x^2-3x+5>=0
отудого x (-oo;+oo)
x^2+√x^2-3x+5 >7+3x
√x^2-3x+5 >7+3x-x^2
x^2-3x+5 >(7+3x-x^2)^2
x^2-3x+5 >x^4-6x^3-5x^2+42x+49
x^4-6x^3-6x^2+45x+44<0
ЗДЕСЬ СВОБОДНЫЙ ЧЛЕН РАВЕН 44 значит делители его 1; 4,11,44
ПОдходит только 4 , значит делим на x-4 , получим
(x+1)(x^2-3x+11)(x-4) <0
отудого только x-1>0
x>-1
ответ
(-oo;-1) U (4;+oo)