{ 25-х² ≥0,
{2x-11>0,
{25-х² ≤ (2х-11) ² .
Решим каждое неравенство системы.
1) 25-х² ≥0,
(5-х)(5+х)≥0, метод интервалов
- - - [-5][5] - - - . Тогда х принадлежит [-5;5].
2) 2x-11>0,
2х>11 , >5,5 .Тогда х принадлежит (5,5 ; + бесконечно).
3) 25-х² ≤ (2х-11) ²
25-х² ≤ 4х²-44 х+1121,
5х²-44 х+96≥0. Найдём нули квадратного трехчлена
5х²-44 х+96=0, D=16, x1=4, x2=4,8.
5(x-4) (x-4,8) ≥0, метод интервалов
[4]- - - - [4,8] . Тогда х принадлежит (- беск;4) и (4,8 ; + беск).
Получили
{-5≤ х≤5,
{ х>55,5 ,
{х<4 х>4,8 ⇒ х принадлежит пустому множеству.
ответ решений нет.
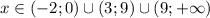
Объяснение:
Перефразируя условие задачи, требуется решить неравенство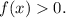 
Для этого стоит воспользоваться методом интервалов. Схематически наносим в правильном порядке на числовую прямую точки, превращающие в ноль каждый из сомножителей числителя и знаменатель: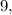 
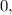
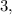
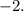Берем любое число правее самого правого (9) и, подставляя в функцию, определяем ее знак. Например, при 
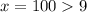знаки всех сомножителей числителя и знаменателя положительны, значит и значение дроби будет положительным. Значит запускаем «змейку» сверху. Проходя через каждую из точек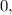 
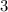и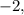 
«змейка» будет менять свое положение относительно числовой прямой. Проходя через точку 9 (за счет четной степени у скобки) — не будет. Действительно, взяв любое значение аргумента в промежутке от 3 до 9 можно проверить, что значение функции останется положительным.
Для ответа нужно перечислить все интервалы, на которых «змейка» находится выше числовой прямой.
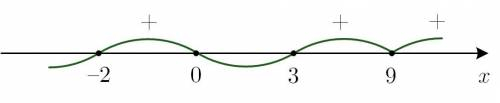
2. Теорема Виета свободный член многочлена равен 0.