Это просто
так как есть х²- это график параболы, при х² нет минуса, значит ветви параболы направлены вверх. Теперь надо найти точку пересечения параболы с осью ОУ .для этого х=0
у=0²-4*0-5=-5 . Точка пресечения с осью ОУ (0;-5)
Теперь найдём точки пересечения с осью ОХ (у=0)
х²-4х-5=0
D= 4²-4*1*(-5)=16+20=36

первая точка пересечения с осью ОХ (-1;0), вторая (5;0)
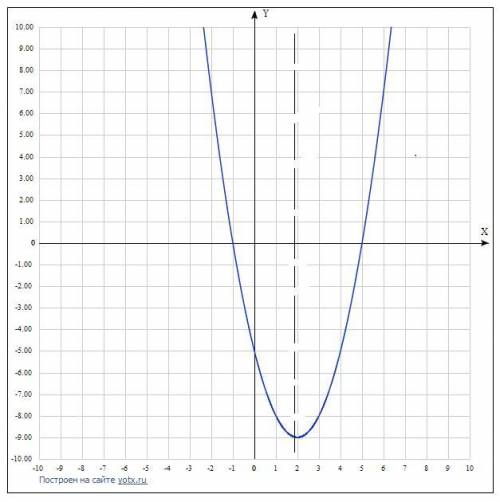
Посередине между этими точками будет ось симметрии параболы ( отметим штрихом на графике)
ну ещё пар точек определим при х=2
у= 2²-4*2-5= -9 точка(2;-9)- вершина параболы
Составим таблицу точек:
х | y
-2 | 7
-1 | 0
0 | 5
1 | -8
2 | -9
3 | -8
4 | -5
5 | 0
6 | 7
В решении.
Объяснение:
Функция задана формулой у=½х(одна вторая икс)+4
А) найдите значение функции, если значение аргумента равно -8
Б) найдите значение аргумента при котором значение функции равно -0,5
В) проходит ли график этой функции через точку А(4;7)?
Дана функция у = х/2 + 4
а) х = -8; у = ?
у = -8/2 + 4
у = -4 + 4
у = 0;
При х = -8 у = 0.
б) у = -0,5; х = ?
-0,5 = х/2 + 4
Умножить уравнение на 2, чтобы избавиться от дроби:
-1 = х + 8
-1 - 8 = х
х = -9;
При х = -9 у = -0,5.
в) у = х/2 + 4; А(4; 7);
7 = 4/2 + 4
7 ≠ 6, не проходит.