Чему равна сумма всех различных значений параметра b, при которых уравнение (b+1)x^2 + 9x + b - 5 = 0 имеет единственный корень?

👇

Ответ:

Dasssshenka

15.03.2021

Чему равна сумма всех различных значений параметра b, при которых уравнение (b+1)x^2 + 9x + b - 5 = 0 имеет единственный корень?
Запишем два условие при которых уравнение (b+1)x^2 + 9x + b - 5 = 0 имеет один корень
1. При b+1=0 или b = -1 уравнение (b+1)x^2 + 9x + b - 5 = 0
превращается в уравнение
9х+ b - 5 =0
которое имеет один корень
х = (5 - b)/9
2. При b=/=-1 уравнение (b+1)x^2 + 9x + b - 5 = 0
имеет один корень при
D =0
D = 81-4(b-5)(b+1) =81-4(b^2 - 4b - 5) = 101 - 4b^2 + 16b
D = 0 или 101 - 4b^2 + 16b =0
4b^2 - 16b - 101 =0
D = 256 + 1616 = 1872
b1=(16-корень(1872)/8 = 2 - (3/2)корень(13)
b2 = (16+корень(1872)/8 = 2 + (3/2)корень(13)
Получили три значения параметра b при которых уравнение имеет один корень.
Сумма этих значений равна
-1+ 2 - (3/2)корень(13) + 2 + (3/2)корень(13) = 3
ответ : 3

4,7(88 оценок)

Открыть все ответы

Ответ:

Дениссирвачак

15.03.2021

1)y`=-2x=0⇒x=0
2)y`=2x+2=0⇒x=-1
   _ +

убыв    -1    возр
х∈(-≈ ;-1)-убыв    х∈(-1;≈)-возр
3)y`=3-3x²=0    3(1-x)(1+x)=0⇒x=1 U x=-1
_ + _

убыв -1 возр    1    убыв
   min    max
4)v(t)=s`(t)=3t²+2 v(1)=3+2=5
a(t)=v`(t)=6t a(1)=6
5)y`=2x-4=0⇒x=2∉[-3;-1]
y(-3)=9+12=21-наиб
y(-1)=1+4=5-наим
6)НЕ НАПИСАЛА У=?
Решать нужно так:
Найти производную. Ее значение при х нулевом-это и есть тангенс угла.Приравнять производную tg60=√3,получим х нулевое.Подставим это значение в саму функцию и получим координату у самой точки .

4,4(9 оценок)

Ответ:

nazhigp08m0u

15.03.2021

Прямые параллельны - это означает, что у них одинаковый угловой коэффициент, то есть одинаковый тангенс угла наклона к оси OX. Иными словами, если мы идем по любой из этих прямых, то сдвинувшись направо, скажем, на 5 единиц, мы поднимемся наверх на одинаковое количество единиц независимо от того, по какой прямой мы двигаемся. Двигаясь по первой прямой из одной отмеченной точки в другую, мы сдвигаемся вправо на 5 единиц и вверх на 2 единицы. А если бы сдвиг направо был бы в два раза больше - на 10 единиц, то вверх мы бы поднялись не на 2 единицы, а на четыре, то есть тоже в два раза больше. Мы видим, что двигаясь уже по второй прямой из одной отмеченной точки в другую, мы поднимаемся вверх на 4 единицы, значит направо мы сдвигаемся на 10 единиц. Значит, p=10.

Если вам скучно было читать мой опус, могу предложить другой веселый. Поскольку тангенс угла наклона первой прямой к оси OX равен 2/5, и прямая пересекает ось OY в точке с координатой 2, эта прямая имеет уравнение 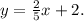$y=\frac{2}{5}x+2.$

Параллельные прямые имеют одинаковые угловые коэффициенты, значит угловой коэффициент второй прямой равен 2/5. Ось OY вторая прямая пересекает в точке с координатой - 4, поэтому уравнение второй прямой 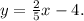$y=\frac{2}{5}x-4.$ Подставив в это уравнение x=p; y=0, получаем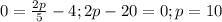 $0=\frac{2p}{5}-4; 2p-20=0; p=10$

Если и это рассуждение вас не вдохновило, посмотрите на два треугольника на вашем чертеже. Они, очевидно, подобны, поэтому мы можем записать отношение соответственных сторон: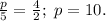 $\frac{p}{5}=\frac{4}{2};\ p=10.$