z=ln(x+e^(-y))
dz/dx=1/(x+e^(-y))*(x+e^(-y))'=1/(x+e^(-y))
d2z/dx2=((x+e^(-y))^(-1))'=-(x+e^(-y))^(-2)*(x+e^(-y))'=-1/(x+e^(-y))^2
d3z/dx2dy=(-(x+e^(-y))^(-2))'=-(-2(x+e^(-y)))^(-3)*(x+e^(-y))'=2(x+e^(-y))^(-3)*(-e^(-y))=-2e^(-y)/(x+e^(-y))^3
dz/dy=1/(x+e^(-y))*(x+e^(-y))'=1/(x+e^(-y))*(-e^(-y))=-e^(-y)/(x+e^(-y))
d2z/dydx=(-e^(-y)*(x+e^(-y))^(-1))'=-e^(-y)*((x+e^(-y))^(-1))'=
-e^(-y)*(-((x+e^(-y))^(-2)))*(x+e^(-y))'=e^(-y)/(x+e^(-y))^2
d3z/dydx2=(e^(-y)/(x+e^(-y))^2)'=e^(-y)((x+e^(-y))^(-2))'=
e^(-y)*(-2((x+e^(-y))^(-3)))*(x+e^(-y))'=-2e^(-y)/(x+e^(-y))^3
и все
-2e^(-y)/(x+e^(-y))^3-(-2e^(-y)/(x+e^(-y))^3)=-2e^(-y)/(x+e^(-y))^3+2e^(-y)/(x+e^(-y))^3=0
Объяснение:
Объяснение:
Для того чтобы показать, что число является составным достаточно показать, что оно у него есть делители помимо 1 и самого себя. Для начала надо понять на какое число заканчивается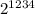
. Для этого нужно понять на какую цифру заканчиваются степени двойки:
Таким образом последняя цифра в степенях двойки может быть только из множества {2, 4, 8, 6}, которое будет циклически повторяться. Дальше надо понять остаток от деления 1234 на 4. 1234 : 4 = 308 и остаток 2. Значит последния цифра у нас совершит 308 полных циклов и еще 2 шага. Таким образом число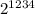
заканчивается на цифру 4. Следовательно 
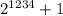заканчивается на цифру 5, а значит это число делится на 5 и как факт является составным.