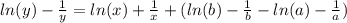Сделаем так чтобы в левой части осталось только dy/dx
Получим
Теперь умножим все на получаем:
Возьмем интеграл от левой и правой части
Находим значения интегралов получаем:
Можно объеденить С и С1 в одну константу, назовем ее С.
Этого я думаю достаточно. Чтобы решить задачу Коши нужны начальные условия, к сожалению здесь они не предоставлены. Поэтому попытаемся решить задачу Коши для произвольных начальных условий
y(a)=b , где a,b-константы
найдем сразу ln(y(a))=ln(b) и подставим все в уравнение
получим
Отсюда
Т.е решеним задачи Коши для произвольных a и b, которые конечно должны принадлежать области определения функций указанных в общем решении уравнения (очевидно, что а и b не равны 0, т.к деление на ноль недопустимо и в общем то говоря а и b>0, если мы конечно не рассматриваем случая когда логарифмическая функция продолжается на комплексное пространство) будет:
1) F`(x)=3x²-6x-9 Находим точки, в которых производная обращается в нуль. F`(x)=0 3x²-6x-9=0 3·(x²-2x-3)=0 x²-2x-3=0 D=16 x₁=(2-4)/2=-1 x₂=(2+4)/2=3 - точки возможных экстремумов Обе точки принадлежат указанному промежутку Не проверяя какая из них точка максимума, какая точка минимума, просто находим F(-4)=(-4)³-3·(-4)²-9·(-4)+35=-64-48+36+35=-41 наименьшее F(-1)=(-1)³-3·(-1)²-9·(-1)+35=-1-3+9+35=40 - наибольшее F(3)=(3)³-3·(3)²-9·(3)+35=8
F(4)=(4)³-3·(4)²-9·(4)+35=64-48-36+35=15
выбираем из них наибольшее и наименьшее
2) F`(x)=3x²+18x-24 Находим точки, в которых производная обращается в нуль. F`(x)=0 3x²+18x+24=0 3·(x²+6x+8)=0 x²+6x+8=0 D=36-4·8=36-32=4 x₁=(-6-2)/2=-4 x₂=(-6+2)/2=-2 - точки возможных экстремумов Обе точки не принадлежат указанному промежутку
Понятно, что в больших коробках и в маленьких коробках количество книг одинаковое и равно половине от общего количества книг (примем за Х). Неодинаково количество больших и маленьких коробок. Пусть больших коробок было А штук, а меленьких В штук. Тогда 24*А - количество книг в больших коробках, 15*В - количество книг в маленьких коробках. И там, и там половина от общего количества книг (по условию). То есть, 24*А = 15*В = Х/2. Мы знаем, что больших коробок на 3 меньше, значит А - 3 = В. Подставим это значение В в наше первое уравнение: 24А = 15(А-3) 24А = 15А-45 А = 5 - столько было больших коробок, а книг в них, соответственно, 120 (24 * 5). Маленьких коробок было 8 (5 + 3), и книг в них тоже 120. Следовательно, всего книг 120 * 2 = 240. ответ: 240 книг.
Разделим все на dx получим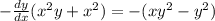
Сделаем так чтобы в левой части осталось только dy/dx
Получим
Теперь умножим все на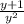 получаем:
получаем:
Возьмем интеграл от левой и правой части
Находим значения интегралов получаем:
Этого я думаю достаточно. Чтобы решить задачу Коши нужны начальные условия, к сожалению здесь они не предоставлены. Поэтому попытаемся решить задачу Коши для произвольных начальных условий
y(a)=b , где a,b-константы
найдем сразу ln(y(a))=ln(b) и подставим все в уравнение
получим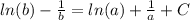
Отсюда
Т.е решеним задачи Коши для произвольных a и b, которые конечно должны принадлежать области определения функций указанных в общем решении уравнения (очевидно, что а и b не равны 0, т.к деление на ноль недопустимо и в общем то говоря а и b>0, если мы конечно не рассматриваем случая когда логарифмическая функция продолжается на комплексное пространство) будет: