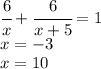
 ,
, , a
, a 
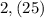
 целая часть. У нас она равна 2
целая часть. У нас она равна 2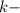 - количество цифр в периоде. У нас их 2
- количество цифр в периоде. У нас их 2 количество цифр до периода. У нас их 0
количество цифр до периода. У нас их 0 все цифры, включая период, в виде натурального числа. У нас это 25
все цифры, включая период, в виде натурального числа. У нас это 25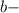 все цифры без периода в виде натурального числа. Их нет.
все цифры без периода в виде натурального числа. Их нет.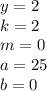
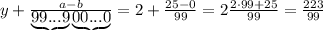
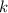 подставляется количество 9, а под
подставляется количество 9, а под  -количество нулей. У нас
-количество нулей. У нас 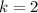 , значит пишем две цифры 9, а
, значит пишем две цифры 9, а  , значит, нулей не пишем вообще. Между
, значит, нулей не пишем вообще. Между 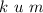 не стоит знак умножения
не стоит знак умножения
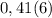
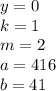

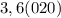

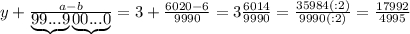
∀a ∈ ℝ: {a} ∈ [0; 1) ⇒ {x} - 1 ∈ [-1; 0).
∀a ∈ ℝ: [a] ∈ ℤ ⇒ [x] + ... + [x²⁰⁰³] ∈ ℤ.
Но [x] + ... + [x²⁰⁰³] = {x} - 1. Значит, {x} - 1 ∈ ℤ ∩ [-1; 0), то есть {x} - 1 = -1, или {x} = 0 ⇔ x ∈ ℤ.
Теперь переформулируем задачу.
Найдите все целые решения уравнения x²⁰⁰³ + ... + x + 1 = 0.
По следствию из теоремы Безу целые корни многочлена должны являться делителями свободного члена. В нашем случае свободный член - 1. У него два делителя: 1 и -1. Очевидно, что 1²⁰⁰³ + ... + 1 + 1 ≠ 0, а (-1)²⁰⁰³ + ... + (-1) + 1 = 0. Значит, имеем корень, равный -1. Других целых решений, как оговаривалось ранее, нет.
ответ: x = -1.
Скорость от станции до почты =(х+5) км/час
Время на весь путь равно сумме времени
Отрицательное значение не подходит.
ответ: 15 км/час