Событие A₁- " первая деталь имеет дефект"
Противоположное ему событие:
Â₁- " первая деталь не имеет дефекта"
Событие A₂- " вторая деталь имеет дефект"
Противоположное ему событие:
Â₂- " вторая деталь не имеет дефекта"
и так далее
до (N+3) cобытия
A(N+3)-" N+3-я деталь имеет дефект"
Â(N+3)-" N+3-я деталь не имеет дефекта"
a) A-" ни одна из деталей не имеет дефекта
A=Â₁∩Â₂·∩..∩Â(N+3)
б)В-"по крайней мере одна из деталей имеет дефект"
B=(A₁∩Â₂·∩..∩Â(N+3)∪Â₁∩А₂∩..∩Â(N+3)∪...∪Â₁∩Â₂∩..∩А(N+3))∪
∪(A₁∩А₂∩..∩Â(N+3)∪Â₁∩А₂∩А₃∩..∩Â(N+3)∪...∪Â₁∩Â₂...∩А(N+2)∩А(N+3))∪
∪...(A₁∩A₂·∩..∩A(N+3))
в)C-" только одна из деталей имеет дефект"
С=A₁∩Â₂·∩..∩Â(N+3)∪Â₁∩А₂∩..∩Â(N+3)∪...∪Â₁∩Â₂∩..∩А(N+3)
г) D-"не более двух деталей имеют дефект
Значит две, одна или ни одной:
D=(A₁∩А₂∩..∩Â(N+3)∪Â₁∩А₂∩А₃∩..∩Â(N+3)∪...∪Â₁∩Â₂...∩А(N+2)∩А(N+3))∪
(Это две1 и 2; 1и 3; ... предпоследняя и последняя)
∪(A₁∩Â₂·∩..∩Â(N+3)∪Â₁∩А₂∩..∩Â(N+3)∪...∪Â₁∩Â₂∩..∩А(N+3))∪
(Это одна; 1 или вторая 2или ... последняя)
∪(Â₁∩Â₂·∩..∩Â(N+3))
(это событие А - ни одна из деталь не имеет дефекта, все без дефекта)
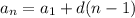
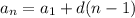
Пусть x - скорость второго туриста, тогда (x+3) - первого.
Получаем равенство:
30/(x+3)=20/x+1/3
Приведем к общему знаменателю и перенесем выражение с правой части - в левую:
30x/x(x+3)-20(x+3)/x(x+3)=1/3,
(30x-20x-60)/x(x+3)=1/3,
(10x-60)/x(x+3)=1/3,
x(x+3)=3(10x-60),
x^2+3x-30x+180=0,
x^2-27x+180=0
Найдем дискриминант:
Д=27*27-4*180=9
x1=(27+3)/2=15, x2=(27-3)/2=12
скорость первого - 15 км/ч, второго - 12 км/ч
Тогда t1=30/15=2 ч, а t2=20/12=1 2/3 ч
ответ: t1=2 ч, t2=1 2/3 ч