Решение во вложении:
............................
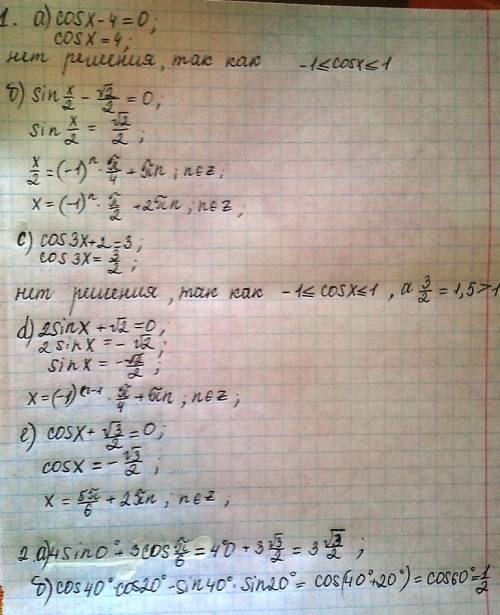
строим график функции
у= х^3 кубическая парабола
х=0 , у= 0^3 = 0 ( 0, 0 ) 1 точка
х=1 , у= 1^3 = 1 ( 1 , 1 ) 2 точка
все остальные точки находят по этому прнципу. Пишу уже готовые точки
х 0 1 2 -1 -2
у 0 1 8 -1 -8
строим график у= -х это прямая
нужно найти только 2 точки, но я найду 4 для удобства построения
у= -х
х= 1 , у = -1 ( 1 , -1) 1 точка
х=2 , у= -2 ( 2 , -2) 2 точка
х= -1 , у= - ( -1) = 1 ( -1 , 1 ) 3 точка
х= -2 , у= - ( -2) = 2 ( -2 , 2) 4 точка
х 1 2 -1 -2
у -1 -2 1 2
точка пересечения двух графиков ( 0 , 0 )
как находить точки можешь не писать , а сразу таблицу с точками.
А) Первая бригада за шесть дней выполняет всё задание; значит, за один день она выполнит 1/6 часть задания.
Вторая бригада за десять дней выполняет всё задание; значит, за один день она выполнит 1/10 часть задания.
За 4 дня первая бригада выполнит 1/6 * 4= 4/6=2/3 часть задания.
За 3 дня вторая бригада выполнит
1/10 * 3=3/10 часть задания.
Работая 7 дней раздельно они выполнят
2/3 + 3/10=(2*10+3*3)/3*10=29/30 часть задания. Значит, всё задание выполнено не будет (1/30 часть задания сделано не будет).
Б) первая бригада за 1 день делает
1/6 часть задания; вторая бригада за 1 день делает 1/10 часть задания;
вместе за 1 день делают
1/6 + 1/10=(10+6)/6*10=16/60=4/15 часть задания;
а всё задание вместе сделают за
1 : 4/15=15/4 дня; в день они работают по 8 часов (48:6=8; 80:10=8); значит всё задание вместе они сделают за 15/4 * 8=15*2=30 часов.
ЕСЛИ НЕ СЛОЖНО ТО ОТМЕТЬ, КАК ЛУЧШИЙ ОТВЕТ
а) cosx-4=0
cosx=4
решений нет, т.к. |cosx|<=1, а 4>1
b) sin x/2-sqrt{2}/2=0
sinx/2=sqrt{2}/2
x/2=(-1)^n *pi/4 +pi*n
x=(-1)^n *pi/2 +2pi*n, n принадлежит Z
c)cos 3x+2=3
cos3x=3/2
решений нет, т.к. |cos3x|<=1 а 3/2=1,5>1
d) 2sinx+ sqrt{2}=0
2sinx=-sqrt{2}
sinx=-sqrt{2}/2
x=(-1)^(n-1)*pi/4+pi*n,n принадлежит Z
e) cosx+sqrt{3}/2=0
cosx=-sqrt{3}/2
x=pi-pi/6 +2pi*n
x=5pi/6 +2pi*n, n принадлежит Z
a) 4sin0+3 cos (pi/6) =4*0+3sqrt{3}/2=3sqrt{3}/2
b) cos 40 cos 20-sin 40sin 20=cos(40+20)=cos60=1/2