
a|x|<0
для будь-якого х: |x|>=0;
тому якщо a>0 нерівність a|x|<0 розвязку немає, зліва додатна величина
якщо а=0, то нерівність має вигляд 0х<0, яка розвязків немає
якщо a<0, то a|x|<0 рівносильна нерівності |x|>=0 і її розвязком буде будь-яке дійсне число
обєднуючи якщо a>=0 то розвязку немає,
якщо a<0, то розвязкок - будь-яке дійсне число, (x є R, x є 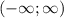 ))
))
x(6-x квадрате)>0
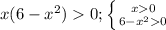
чи 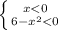
розвязуємо першу систему
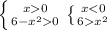
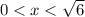
розвязуємо другу систему
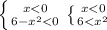
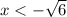
обєднуючи х є [tex] (-\infty; -\sqrt{6}) \cup (0;6)}
Объяснение: