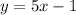
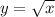
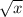 имеет смысл только при х≥0, то
имеет смысл только при х≥0, то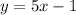 Множество значений - все действительные числа:
Множество значений - все действительные числа: 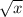 Множество значений - это также множество всех неотрицательных чисел: Е(f) = [ 0; + oo )
Множество значений - это также множество всех неотрицательных чисел: Е(f) = [ 0; + oo )
(5x + 6)⁴ + 5(5x + 6)² - 6 = 0.
Обозначим (5x + 6)² = у и перепишем уравнение в виде
у² + 5у - 6 = 0.
D = 5² - 4 · 1 · (-6) = 25 + 24 = 49; √49 = 7.
у₁ = (-5 + 7)/(2 · 1) = 2/2 = 1, у₂ = (-5 - 7)/(2 · 1) = -12/2 = -6.
Вернемся к обозначениям:
(5x + 6)² = -6 - не имеет решений, т.к. квадрат выражения не может быть отрицательным.
(5x + 6)² = 1,
25х² + 60х + 36 = 1,
25х² + 60х + 36 - 1 = 0,
25х² + 60х + 35 = 0,
5х² + 12х + 7 = 0,
D = 12² - 4 · 5 · 7 = 144 - 140 = 4; √4 = 2.
х₁ = (-12 + 2)/(2 · 5) = -10/10 = -1
х₂ = (-12 - 2)/(2 · 5) = -14/10 = -1,4
ответ: -1,4 и -1.
где х, y - некоторые натуральные числа
Предположим что
тогда из второго соотношения (2) следует что
где k - некоторое натуральное число
откуда
а значит число |16a-9b| сложное если
и
Рассмотрим варианты
1)
что невозможно - два последовательных натуральных числа не могут быть квадратами натуральных чисел
(доказательство єтого факта
=>x=1; y=0
)
2)
=> k - ненатуральное -- невозможно
3)
=> k - ненатуральное - невозможно
тем самым окончательно доказали,что исходное утверждение верно.
Случай когда
Учитывая симметричность выражений a+b=b+a, ab=ba
доказывается аналогично.
Доказано