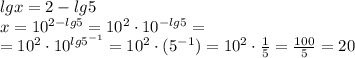
1
Объяснение:
Угол наклона прямой в координатной плоскости изменяется в промежутке [0; π) за исключением π/2, то есть по значению тангенса можно однозначно определить угол. Вспомним, что прямые параллельны, если соответственные углы равны. Если принять за секущую ось Ox, то можно сравнить углы наклона. А для этого уже достаточно сравнить их тангенсы!
Тангенс угла наклона касательной можно найти с производной — это значение производной в данной точке. Тангенс угла наклона прямой — это коэффициент перед x. Тогда:
— если подставить вместо x какое-то значение, получим тангенс угла наклона касательной. Тангенс угла наклона прямой — это 1 (y = 1*x + 8). Поэтому, чтобы прямые были параллельны, нужно приравнять производную и тангенс угла наклона прямой:
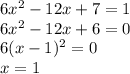
Пусть будет x коробок по 90 р и y коробок по 50 р.
Всего истратили 1300 р.
90x + 50y = 1300
9x + 5y = 130
Это так называемое диофантово уравнение, то есть с несколькими переменными. Его нужно решить в натуральных числах.
Применим такой прием.
y = (130 - 9x)/5 = 26 - (5x + 4x)/5 = 26 - x - 4x/5
Чтобы у было натуральным, х должно делиться на 5.
Решения: 1) x = 5, y = 26 - 5 - 4*1 = 17; Всего 5 + 17 = 22 коробки.
2) x = 10, y = 26 - 10 - 4*2 = 8; Всего 10 + 8 = 18 коробок.
Других вариантов нет.
ответ: наибольшее число коробок 22.
