y=cos(x+π/2)-1
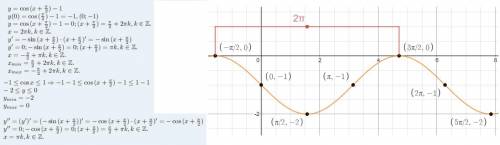
График этой функции будет выглядеть как косинус х, только он будет опущен на 1 и сдвинут влево на π/2. Это я про то, что можно сдвигать график по осям и строить последовательно, а можно сразу всё найти как я сейчас и сделаю, таким образом просто быстрее искать нули т.д. если ты не помнишь какие нули и экстремумы у обычного косинуса. Найдём всё, что надо для построения и построим.
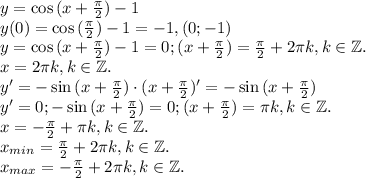
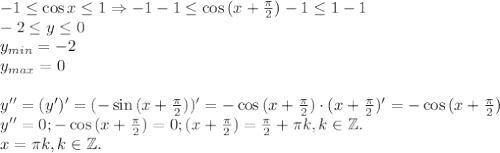
Ордината точки перегиба будут -1 т.к. это косинус и его значение от -2 до 0. У нас есть всё, чтобы построить график, мы знаем что это график косинуса, поэтому нам известно как именно выпукла функция, что у неё есть период и т.д. Кстати период у функции 2π.
Внизу смотри вычисления и график функции.
Из свойства модуля действительного числа имеем:
Так как мы ищем решения нашего уравнения при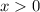 , тогда (1) примет вид
, тогда (1) примет вид 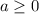 -----(2)
-----(2)
Раскроем знак модуля:
а) Если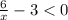 ---------(1а)
---------(1а)
то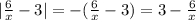 -------(2а)
-------(2а)
При этом решением неравенства (1а) является объединение числовых промежутков:
Исходное уравнение с учетом (2а) примет вид:
Чтобы уравнение (*) имело хотя бы один корень, его дискриминант должен быть неотрицательный:
б) Если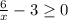 ---------(1б)
---------(1б)
то модуль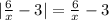 ---------(2б)
---------(2б)
При этом решением неравенства (1б) является числовой полуинтервал:
Исходное уравнение с учетом (2б) примет вид:
Чтобы уравнение (**) имело хотя бы один корень, его дискриминант должен быть неотрицательный: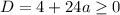 , отсюда
, отсюда
Но вначале мы показали, что параметр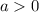
А это значит, что квадратное уравнение (**) при всех положительных значениях параметра уравнение имеет два корня.
Но так как мы ищем решения на промежутке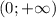 , то исходное уравнение будет иметь 3 или 4 корня, если значения параметра
, то исходное уравнение будет иметь 3 или 4 корня, если значения параметра  будут удовлетворять двойному неравенству:
будут удовлетворять двойному неравенству: