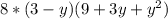1. Чтобы начертить графики, необходимо составить таблицу значений для каждого выражения для соответствующих значений x:
x2+6x+8,еслиx∈[−6;−1].
x
−6
−5
−4
−3
−2
−1
y
x+2−−−−√+2,еслиx∈(−1;2].
x
−1
0
1
2
y
2. Заполняем обе таблицы значениями y, которые можно вычислить, подставив в выражение вместо x соответствующие значения аргумента:
x2+6x+8,еслиx∈[−6;−1];
a) y=(−6)2+6⋅(−6)+8=36−36+8=8;
b) y=(−5)2+6⋅(−5)+8=25−30+8=3;
c) y=(−4)2+6⋅(−4)+8=16−24+8=0;
d) y=(−3)2+6⋅(−3)+8=9−18+8=−1;
e) y=(−2)2+6⋅(−2)+8=4−12+8=0;
f) y=(−1)2+6⋅(−1)+8=1−6+8=3.
x
−6
−5
−4
−3
−2
−1
y
8
3
0
−1
0
3
x+2−−−−√+2,еслиx∈(−1;2];
y=−1+2−−−−−−√+2=1–√+2=1+2=3;
y=0+2−−−−√+2=2–√+2≈1,41+2≈3,41;
y=1+2−−−−√+2=3–√+2≈1,73+2≈3,73;
y=2+2−−−−√+2=4–√+2=2+2=4.
x
−1
0
1
2
y
3
3,41
3,73
4
3. Чертим график функции.
a4.png
При значении x, равном −1, по интервалу первого выражения точка должна быть закрашенной, но по интервалу второго выражения точка должна быть незакрашенной. В этой ситуации точка на чертеже должна быть закрашенной.
4. Интервалы возрастания и убывания функции определяем по оси x. Если при возрастании значений x значения функции возрастают (на рис. график идёт вверх), то на этом интервале функция возрастает. Если при возрастании значений x значения функции убывают (на рис. график идёт вниз), то на этом интервале функция убывает.
a4.png
Интервал возрастания функции: x∈[−3;2].
Интервал убывания функции: x∈[−6;−3].
5. Точку, в которой функция непрерывна и меняется с возрастающей на убывающую, называют максимумом функции. Точку, в которой функция непрерывна и меняется с убывающей на возрастающую, называют минимумом функции. Минимумы и максимумы функции называются экстремумами. Поэтому экстремумом функции является f(−3) = −1 (минимум функции).
6. Наибольшее и наименьшее значения функции находят по оси y, и они часто совпадают с экстремумами функции. Разница в том, что наибольшее и наименьшее значения есть в том случае, когда функция прерывается. В данном примере наибольшим значением функции является f(−6) = 8, наименьшим значением функции является f(−3) = −1.
7. Положительные и отрицательные значения функции определяют по оси x. Та часть функции, график которой находится ниже оси x, является отрицательной, а та, которая находится выше оси x, является положительной. Следовательно, функция положительна, если x∈[−6;−4)∪(−2;2], и отрицательна, если x∈(−4;−2).
8. Так как функция не симметрична ни относительно оси y , ни относительно начала координат, то она является ни чётной, ни нечётной.
9. Нулями функции являются те значения, при которых функция касается или пересекает ось x:
x1=−4,т. к.f(−4)=0;
x2=−2,т. к.f(−2)=0.
10. Точки пересечения с осями x и y можно определить по графику:
a) точки пересечения с осью x: (−4;0) и (−2;0);
б) точка пересечения с осью y: (0;3,41).
Объяснение:
По формуле разности кубов: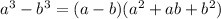
ответ: