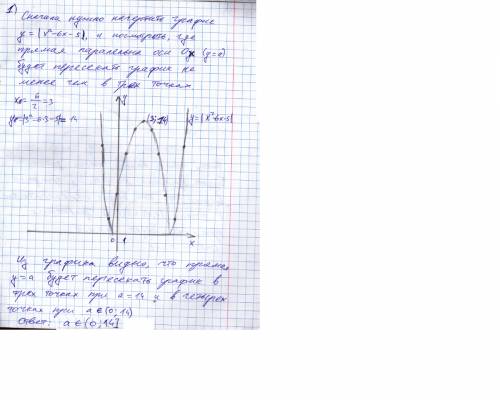
1) квадратное уравнение с модулем будет иметь не менее трех корней если прямая а проходит через вершину параболы -(x^2-6x-5) - это верхнее значение параметра,
а нижнее а=0.
находим вершину параболы, х0=-b/2a у нам b=6 a=-1 x0=3
y0=-9+5+18=14
значит а [0;14]
2) sqrt(x-1)=a+x x>=1
x-1=x^2+a^2+2ax
x^2+(2a-1)x+a^2+1=0
D>0 (2a-1)^2-4a^2-4>0 -4a-3>0 a<-3/4
3) 4x^2-15x+4a^3=0
x1=x2^2
x1*x2=a^3
x2^3=a^3 x2=a
15/4=x1+x2 15/4=a^2+a
4a^2+4a-15=0 a1=3/2 a2=-5/2
x^2-ax+(a-1)=0
x1^2+x2^2=(x1+x2)^2-2x1x2=17
a^2-2(a-1)=17
a^2-2a-15=0
a1=5 a2=-3



Перейдем в исходном уравнении от корней к степеням с дробным показателем, тогда уравнение примет вид:
В получившемся уравнении перемножим степени в скобках как степени с одинаковым основанием, получим в результате равносильное уравнение:
Отсюда по свойству степеней получим равносильное уравнение, применив свойство степень в степени:
Сделаем замену в последнем уравнении: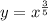
Тогда последнее уравнении примет вид:
Замечаем, что новая неизвестная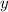 должна удовлетворять условию:
должна удовлетворять условию:
Возведем обе части уравнения в квадрат, после приведя подобные, получим квадратное уравнение:
Для нахождения корней квадратного уравнения воспользуемся теоремой Виета:
Отсюда получим искомые корни:
При этом корень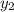 посторонний, поскольку не удовлетворяет не равенству (2). Таким образом, исходное уравнение имеет один корень:
посторонний, поскольку не удовлетворяет не равенству (2). Таким образом, исходное уравнение имеет один корень:
Вернем к старой неизвестной, получим:
ответ: