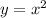
Объяснение:
ДУМАЕМ Площадь фигуры - интеграл разности функций.
Рисунок к задаче в приложении.
РЕШЕНИЕ
1) Находим точки пересечение = пределы интегрирования.
x² - 4*x + 1 = x + 1 превращается в квадратное уравнение:
x²- 5*x = x*(x - 5) = 0
b= 0 - нижний предел и а = 5 - верхний передел интегрирования.
Находим интеграл разности функций: s = 5*x - x² - прямая выше параболы.
S=
Мне нравится именно такая запись решения интеграла - увеличиваем степень и на неё же и делим.
Вычисляем на границах интегрирования.
S(5) = 62 1/2 - 41 2/3 = 20 5/6, S(0) = 0.
S = S(5) - S(0) = 20 5/6 - площадь фигуры - ОТВЕТ (≈ 20,833)
2 (км/час) - скорость течения реки.
Объяснение:
Катер проплив 48 км за течією річки і повернувся назад, витративши на весь шлях 7 год. Знайдіть швидкість течії річки, якщо власна швидкість катера дорівнює 14 км/год.
Формула движения: S=v*t
S - расстояние v - скорость t – время
х – скорость течения реки.
14+х – скорость катера по течению.
14-х – скорость катера против течения.
48/(14-х) – время катера против течения.
48/(14+х) – время катера по течению.
На весь путь туда и обратно потрачено 7 часов.
По условию задачи составляем уравнение:
48/(14+х) + 48/(14-х) = 7
Общий знаменатель (14+х)(14-х), надписываем над числителями дополнительные множители, избавляемся от дроби:
48*(14-х) + 48*(14+х) = 7(196-х²)
672-48х+672+48х=1372-7х²
7х²=1372-1344
7х²=28
х²=4
х= ±2, но отрицательное значение отбрасываем.
х=2 (км/час) - скорость течения реки.
Проверка:
48:16 + 48:12=3+4=7 (часов), верно.
сначала надо сделать так чтобы у была равно строго нулю