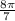 ))
))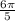 ))
))По теореме косинусов
64*3 = r^2 + r^2 - 2* r^2 * cos 120
192 =2 * r^2 + 2 * r^2* cos 60
192 =2 * r^2 + 2 * r^2* 1/2
192 = 3* r^2
r^2 = 64 см
r = 8 см
Из треугольника АОС, т к. угол осевого сечения при вершине С равен 90 градусов
угол САО = угол ОСА = 45 гр. , следовательно СО =ОА = 8 см
Из треугольника ОВК:
ОК = (64 — 16*3)^(1/2) = 4
Из треугольника КОС
КС = (СО^2 + OR^2)^(1/2) = (64 +16)^(1/2) = 4*(5)^(1/2)
Итак, искомая площадь
S = 1/2*AB*CK = 1/2 * 8*(3)^(1/2)*4*(5)^(1/2) = 16*(15)^(1/2) cм^2
ответ: S = 16*(15)^(1/2) cм^2
Объяснение:
по формулам приведения:
Также необходимо знать, что
Но -9π/14 не находится на отрезке от 0 до π. A 9π/14 как раз принадлежит этому отрезку. Значит воспользуемся свойством четности косинуса:
cos(-x)=cosx
Тогда продолжая цепочку, получаем:
-7π/10 не принадлежит интервалу от -π/2 до π/2. Воспользуемся свойством периодичности тангенса:
tgx=tg(x±π)