Решить четыре выражения. а.) -18sin160 градусов / sin 80 градусов * sin 10 градусов б.) 12sin 56 градусов * cos 56 градусов/ sin 112 градусов в.) 4sin 144 градусов * сos 144 градусов / sin 288 градусов г.) 14sin 409 градусов / sin 49 градусов

👇

Ответ:

vikulyaKuzmina

18.04.2022

С первым что-то не знаю, остальные получились сразу
б) $\frac{12sin56*cos56}{sin112} = \frac{6sin112}{sin112} =6$
в) $\frac{4sin144*cos144}{sin288} = \frac{2sin288}{sin288} =2$
г) $\frac{14sin409}{sin49} = \frac{14sin(360+49)}{sin49} =14$

4,6(3 оценок)

Открыть все ответы

Ответ:

LuckyZhenya

18.04.2022

ЗАДАЧА:

Расстояние от точки А до точки В= 62 км. На расстоянии 30 км от точки А находится точка С. Из точки А в точку С выехал велосипедист со скоростью 12км/ч, а через 30 минут из точки В в точку С выехал мотоциклист.

ВОПРОС 1: с какой скоростью должен ехать мотоциклист, чтобы встретиться с велосипедистом в точке С?

ВОПРОС 2:

С какой скоростью должен ехать мотоциклист, чтобы приехать в точку С раньше велосипедиста на 1 час 10 минут?

Объяснение:

если от точки А до точки С 30км, то от точки

С до В=62–30=32км. Поэтому велосипедисту до точки С нужно проехать 30км, а мотоциклисту из точки В до точки С - 32 км

Велосипедист со скоростью 12км/ч проедет расстояние 30км за: 30÷12=5/2=2,5 часа

1 ч 10 мин=1 целая 1/6часа или 7/6часа.

Чтобы мотоциклист доехал до точки С раньше велосипедиста на 7/6часа, тогда:

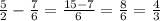
$\frac{5}{2} - \frac{7}{6} = \frac{15 - 7}{6} = \frac{8}{6} = \frac{4}{3}$

Итак: мотоциклисту нужно добраться до точки С за 4/3 часа. Для этого ему понадобится:

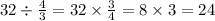
$32 \div \frac{4}{3} = 32 \times \frac{3}{4} = 8 \times 3 = 24$

ОТВЕТ 2: мотоциклисту нужно ехать со скоростью 24км/ч, чтобы приехать раньше велосипедиста на 1 час 10 минут.

РЕШЕНИЕ Вопроса 1

30минут=1/2=0,5 часа

Так как мотоциклист выехал через 30 минут после

велосипедиста, то велосипедист за 30 минут проехал: 12÷2=6км и ему осталось проехать 30–6=24км и ему понадобится на это:

2,5 –0,5=2часа.

Соответственно мотоциклисту до встречи с велосипедистом в точке С понадобится также 2часа.

Мотоциклисту нужно за 2 часа проехать 32 км, поэтому ему нужно ехать со скоростью: 32÷2=16км/ч

ОТВЕТ 1: чтобы встретиться с велосипедистом в точке С мотоциклисту нужно ехать со скоростью 16км/ч

4,6(19 оценок)

Ответ:

sasha200121

18.04.2022

1) Подставим корень в уравнение

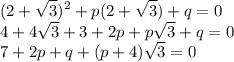
$\displaystyle\\(2+\sqrt{3})^2 + p(2+\sqrt{3}) + q = 0\\4+4\sqrt{3}+3+2p+p\sqrt{3} + q =0\\7+2p+q + (p+4)\sqrt{3} = 0$

Так как p и q - целые, а корень из трех вообще иррациональный, никаким домножением на целое число его не сделать целым. Если только не умножать на 0. Поэтому

p = -4

7+2p+q = 0

q = 1

2) Подставим корни p и q в это уравнение. Имеем

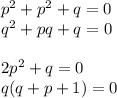
$p^2+p^2+q = 0\\q^2+pq+q = 0\\\\2p^2 + q =0\\q(q+p+1) = 0$

Либо q = 0 и p = 0

Либо p = -q-1 ≠ 0 и тогда

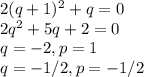
$2(q+1)^2+q=0\\2q^2 + 5q+2=0\\q = -2, p = 1\\q = -1/2, p =-1/2$

Второй вариант не подойдет, потому что у получающегося уравнения есть только один корень -1/2, но второй с ним не совпадает

3) Пусть меньший корень равен p, тогда больший - 2p.

Очевидно a = 0 не подходит, имеем после подстановки

$p^2-pa+2a-4 = 0\\4p^2-2pa+2a-4 = 0\\\\4p^2-4pa+8a-16=0\\4p^2-2pa+2a-4 = 0\\2pa - 6a + 12 = 0\\pa = 3a-6\\p = 3-6/a$

Отметим что a не может равняться двум, потому что тогда 2p = p=0, а при a=2 корни уравнения 0 и 2.

Подставим этот корень в исходное уравнение

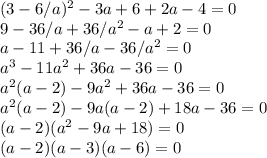
$(3-6/a)^2 - 3a+6+2a-4 = 0\\9-36/a+36/a^2 - a + 2=0\\a-11+36/a-36/a^2=0\\a^3-11a^2+36a-36=0\\a^2(a-2) - 9a^2+36a-36=0\\a^2(a-2) - 9a(a-2) + 18a-36=0\\(a-2)(a^2-9a+18) = 0\\(a-2)(a-3)(a-6)=0$

Почему надо пытаться вынести a=2? Потому что при a=2 формально p=2p, и значит у полученного кубического уравнения a=2 должно быть корнем. Но нас интересуют другие a

a = 3, x^2-3x+2, корни 1 и 2

a = 6, x^2-6x+8, корни 2 и 4

ответ: при a = 3 или 6

4,7(55 оценок)

Это интересно:

Стиль-и-уход-за-собой

11.01.2023

10 способов развить чувство стиля: от выбора базовых вещей до экспериментов со стилем...

Здоровье

27.08.2022

Естественные способы лечения нарколепсии...

Образование-и-коммуникации