104.
a) cos 120 =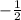 
б) sin(-150)= -sin 150=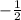
в) tg(-225)= -tg 225 = -1
г) cos(-225)=cos 225=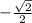 
д) cos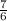 
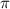= cos 630 = 0
е)sin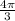 
= sin 240 =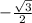
106.
а) sin (
-
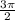) = sin (-270) = sin (270-) = -cos
б) cos (-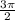)= cos (-270) = cos (270-) = -sin
в) tg (-2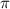) = tg (-360) = tg (360-) = -tg
Объяснение:
104.
cos(-α)= cos α
sin(-α)= -sin α
tg(-α)= -tg α
ctg(-α)= -ctg α
a) cos 120 =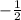
б) sin(-150)= -sin 150= 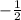( т.к. sin непарная функция => sin(-α)= -sin α )
в) tg(-225)= -tg 225 = -1 ( т.к. tg непарная функция => tg(-α)= -tg α )
г) cos(-225)=cos 225= 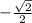( т.к. cos парная функция => cos(-α)= cos α )
д) cos =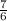 
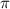=630, 630=360+270 ( 360 это один полный оборот)
=> cos 270 cos 270 = 0
е)sin 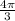= sin 240 =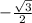
106.
В этом номере я использовал формулы приведения
их можно найти в интернете
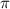=180°
а) sin (-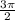) = sin (-270) = sin (270-) = -cos
б) cos (-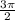)= cos (-270) = cos (270-) = -sin
в) tg (-2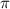) = tg (-360) = tg (360-) = -tg
судя по заданию-график построен y=x^2-6x
решением неравенства
y<=x^2-6x- будет внешняя часть параболы, включая саму параболу. Если вы затрудняетесь с ее определением-совет: берите точку C (7;0) и подставляйте в неравенство
0<=49-42-верно. значит внешняя часть параболы, куда входит C (7;0)-решение. Сама парабола тоже решение- так как неравенство нестрогое. Область решения неравенства выделили штриховкой . как показано на чертеже.
По поводу точек А и В -поставлю их в плоскости рисунка.
А входит во внутреннюю область параболы-значит не является решением, В-во внешнюю, область штриховки, значит решение неравенства.