3. Дана функция f(x) = -x2 + 4x -3 а) Найдите координаты вершины параболы
б) Запишите уравнение оси симметрии графика данной функции
в) Найдите точки пересечения графика функции с осью ОХ
г) Найдите точки пересечения графика функции с осью OY
д) Постройте график функции
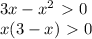
y' = x²-2x = х(х-2) = 0.
Отсюда 2 корня: х₁ = 0
х₂ = 2.
Теперь надо определить, где минимум, а где максимум,
Если при прохождении через критическую точку производная меняет знак с минуса на плюс, то есть это будет минимум, а если меняет знак с плюса на минус, соответственно это будет максимум.
Найдём значения производной при х = -1 и х = 1
х = -1 y' = (-1)²-2*(-1) = 1+2 = 3.
x = 1 y' = 1²-2*1 = 1-2 = -1.
Знак меняется с + на - (это максимум).
Так же надо поступить и с второй точкой.
В приложении даётся график для наглядности определения точек.