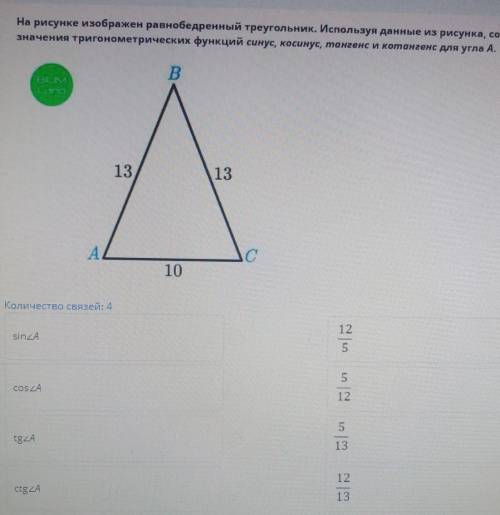
(x³ + 1)/(x + 1) + 3/(x² - x + 1) ≤ 4
одз x≠-1
да и сократим первyю дробь
(x² - x + 1) + 3/(x² - x + 1) ≤ 4
(x² - x + 1) всегда положителен D<0 и коэффициент при х^2 больше 0
приводим к общему знаменателю и отбрасываем его(он всегда положителен)
(x² - x + 1)² - 4(x² - x + 1) + 3 ≤ 0
D = 16 - 12 = 4
(x² - x + 1)₁₂ = (4 +- 2)/2 = 1 3
(x² - x + 1 - 1)(x² - x + 1 - 3) ≤ 0
(x² - x)(x² - x - 2) ≤ 0
вторая скобка D=1+8 = 9 x12=(1+-3)/2 = 2 -1 x² - x - 2 = (x - 2)(x + 1)
x(x-1)(x-2)(x+1) ≤ 0
применяем метод интервалов
[-1] [0] [1] [2]
x ∈ [-1,0] U [1,2]
вспоминаем одз х≠-1
ответ x ∈ (-1,0] U [1,2]
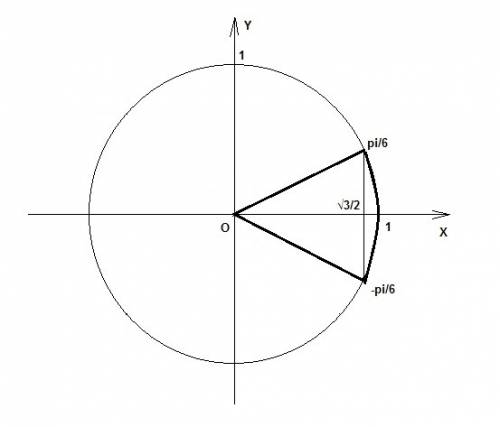
Чтобы найти тригонометрические функции, надо, чтобы треугольник был прямоугольный. Для этого проведем высоту из вершины В на сторону АС. Высота разделит сторону пополам, т.к. треугольник равнобедренный. Половина АС будет катетом прямоугольного треугольника и будет равна 5.
Теперь найдем длину высоты, т.к. это будет второй катет.
По т.Пифагора
13²-5²=144=12²
Длина второго катета равна 12.
А теперь находим тригонометрию для ∠А:
Sin∠A=12/13
Cos∠A=5/13
tg∠A=12/5
ctg∠A=5/12