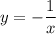и затем верхнюю часть графика отобразить в нижнюю(отрицательную часть)
(*)
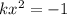и это уравнение решений не имеет при k>0(так как левая часть всегда положительно).
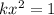и при k<0 это уравнение решений не имеет.
, имеем
∈ 
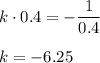
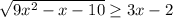
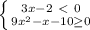
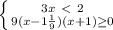
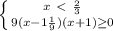
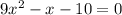
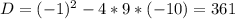
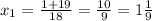
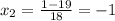
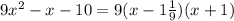
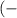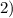
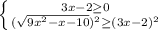
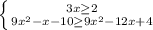
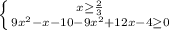
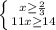
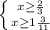
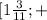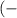∞ ![;-1]](/tpl/images/0674/0179/c47ae.png)
∈ 
∞ 
∈ ∞ ∪ ∞ 
sin²(x-8π)=(-sinx)²=sin²x
cos(16π-x)=cosx
1-cos²(16π-x)=1-cos²x=sin²x
левая часть sin²x=sin²x правая часть