Объяснение:
Общий вид линейной функции: у = kx + b
Коэффициент k в построении графика линейной функции отвечает за угол наклона прямой к положительному направлению оси Ох.
Свободный член b отвечает за смещение графика вдоль оси Оу путем параллельного переноса.
Дано: у = 8х + 3.
а) Чтобы график функции был параллелен графику данной функции, необходимо изменить только свободный член b. Причем число b может быть как положительным, так и отрицательным, либо нулем.
Например,
у = 3х + 17;
у = 3х - 29.
б) Чтобы график функции пересекал график данной функции, у него должен отличаться угол наклона к положительному направлению оси Ох. Следовательно в функции нужно заменить коэффициент а. Свободный член b можно менять, а можно оставить таким, какой он есть.
Например,
у = 7х + 5;
у = -12х - 11.
в) Общий вид линейной функции, график которой проходит через начало координат: у = kx.
Т.е. в формуле отсутствует свободный член b.
Чтобы график функции был параллелен графику данной функции, коэффициент а должен остаться таким же.
-19 = 8x - 3
-8х = -3 + 19
-8х = 16 |:(-8)
x = -2
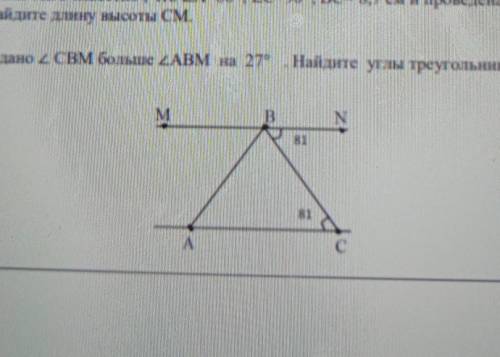
ответ: 81° , 27° , 72° .
Так как ∠АСВ=∠СВN=81° (это внутренние накрест лежащие углы) ,
то MN || AC ⇒ ∠АВМ=∠САВ .
∠СВМ=∠АВМ+∠АВС , то есть можно сказать, что угол СВМ больше
угла АВМ на величину угла АВС .
Из условия задачи следует, что ∠СВМ=∠АВМ+27° , значит ∠АВС=27° .
∠САВ=180°-∠АВС-∠АСВ=180°-27°-81°=72° .