Доказать тождество:
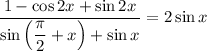
1. Определим область допустимых значений.
1.1. Выражение слева имеет смысл, если его знаменатель не равен нулю:
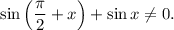
1.2. Используя формулу приведения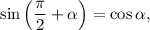 
получаем:
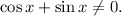
1.3. Умножим обе части на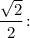 
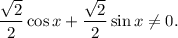
1.4. Поскольку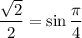 
и 
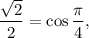то получаем:
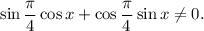
1.5. Используя формулу синуса суммы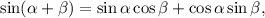 
получаем:
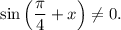
1.6. Так как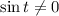 
для 
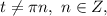то:
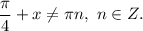
1.7. Перенесём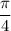 
в правую часть, изменив знак на противоположный:
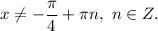
2. Докажем данное тождество, работая с левой частью равенства.
2.1. Преобразуем данное выражение, применив формулу косинуса двойного угла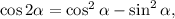 
синуса двойного угла 
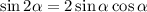и формулу приведения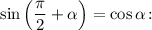 
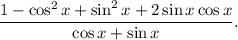
2.2. Замечаем в числителе следствие из основного тригонометрического тождества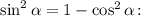 
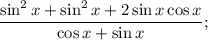
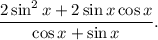
2.3. Вынесем в числителе общий множитель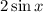 
за скобки:
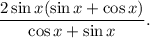
2.4. Сокращаем дробь на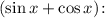 
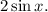
Тождество доказано.
ответ: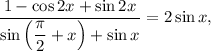 
если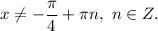
Пометка. Пункт под нахождением области допустимых значений не является обязательным при доказательстве тождества.
Відповідь:
Собственная скорость лодки - 14 км/час.
Пояснення:
Пусть скорость лодки - х, тогда
скорость лодки по течению - ( х + 2 )
скорость лодки против течения - ( х - 2 )
48 / ( х + 2 ) + 24 / ( х - 2 ) = 5
Приведем к общему знаменателю и перенесем его в право.
48х - 96 + 24х + 48 = 5х² - 20
5х² - 72х + 28 = 0
Дискриминант равен
D = 72² - 4 * 5 * 28 = 5184 - 560 = 4624
Корни уравнения равны
х1 = ( 72 + 68 ) / 10 = 14 км/час
х2 = ( 72 - 68 ) / 10 = 0,4 км/час
Второй корень уравнения отпадает, так как если скорость лодки меньше скорости течения, то она не сможет проплыть 24 км против течения.
Проверка.
48 / 16 + 24 / 12 = 3 + 2 = 5
27
Объяснение:
а n = a1 + d (n-1), где n-порядковый номер члена прогрессии.
a5 = 3+6(5-1)=27