• приравниваем (x^2-1)(x+2) к нулю.
• расписываем скобку (х^2-1) по формуле разности квадратов: (х-1)(х+1)
• решаем уравнение относительно х: (х-1)(х+1)(х+2)=0
х-1=0 или х+1=0 или х+2=0
х=1 х=-1 х= -2
• на координатной прямой отмечаем полученные корни: -2; -1; 1
• точки выколотые, так как знак неравенства строгий
• из промежутка от - бесконечность до -2 выбираем любое число, например, -3. Подставляем его в выражение (х^2-1)(х+2): (9-1)(-3+2)= -1*8= -8. Произведение отрицательное, значит на этом промежутке отрицательные значения. Ставим минус.
• так же делаем с каждым промежутком
• ищем промежутки, на которых выражение (х^2-1)(х+2) >0 ( т.е промежутки с «+» )
ответ: х принадлежит (-2;-1) u (1; + бесконечность)
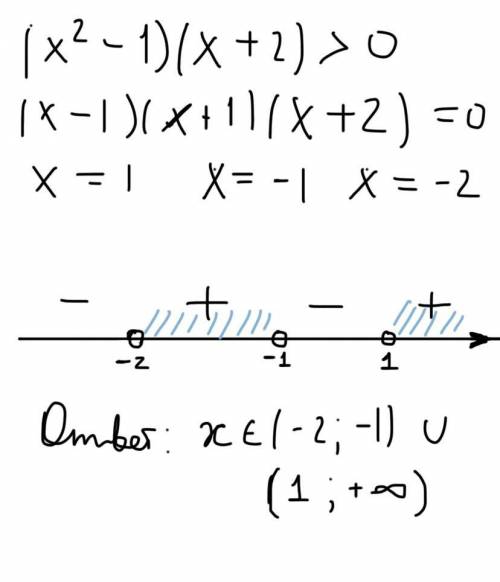
ответ: функция возрастает при x∈(-∞;0)∪(2;+∞)
функция убывает при x∈(0;2)
Объяснение:
берем производную от функции:
y"=2x-16/x²=(2x³-16)/x²
приравниваем к нулю, получаем
x=0 и x=2
функция возрастает на тех промежутках, где производная >0, а убывает на тех промежутках, где производная меньше нуля