ответ: х км/ч - скорость течения
х+11 км/ч - скорость лодки по течению
11-х км/ч - скорость лодки против течения
112/(х+11) ч - время, затраченное лодкой на путь по течению
112/(11-х) ч - время, затраченное лодкой на путь против течения
т.к. время, затраченное на путь по течению, на 6 часов меньше, составляем уравнение
112/(х+11)+6=112/(11-х) *(х+11)(11-х)
112(11-х)+6(11-х)(11+х)=112(11+х)
1232-112х+726-6х^2=1232+112x
6x^2+224x-726=0 :2
3x^2+112x-363=0
D=12544+4356=16900
x1=-121/3 - не подходит
x2=3 км/ч
ответ скорость течения 3 км/ч
Нехай за год перший робітник виконає завдання, а за
год перший робітник виконає завдання, а за 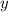 год — другий. Тоді за одну годину перший робітник виконає
год — другий. Тоді за одну годину перший робітник виконає  усього завдання, а другий робітник —
усього завдання, а другий робітник —  .
.
Два робітники, працюючи разом, можуть виконати завдання на 8 год швидше, ніж один перший робітник, тобто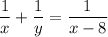
Два робітники, працюючи разом, можуть виконати завдання на 18 год швидше, ніж один другий робітник, тобто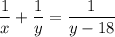
Складаємо систему з двох рівнянь:
Тут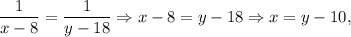 оскільки ліві частини рівнянь рівні.
оскільки ліві частини рівнянь рівні.
Підставимо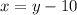 в перше рівняння:
в перше рівняння:
Якщо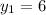 , то
, то  — не відповідає сенсу задачі.
— не відповідає сенсу задачі.
Якщо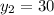 , то
, то 
Отже, за 20 год перший робітник виконає завдання, а за 30 год — другий.
Відповідь: 20 год і 30 год.