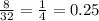Записать формулу зависимости чего-то от чего-то значит записать формулу по которой можно найти первое с второго.
Таким образом, нам надо записать формулу по нахождению d.
d = s - t(v₁ + v₂)
Формула выглядит именно так, потому что d - расстояние между двумя материальными точками (путниками), а оно будет являться не пройденной частью расстояния между селениями. То есть всё расстояние минус то расстояние, которое путники.
Теперь подставим данные, которые представлены в условии:
d = 230 - t( 9 + 5 ) = 230 - 14t
1)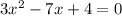
с дискриминанта решать
D= 49-4*3*4=1
тогда x1=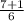 =
=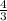
x2= = 1
= 1
2)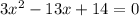
с дискриминанта решать
D= 169-4*3*14=1
тогда x1=
x2=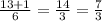
3) мне лень писать пример
с дискриминанта решать
D= 36-4*5*1=36-20=16 - это 4 в квадрате
тогда y1=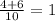
y2=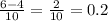 aa
aa
d
4) мне лень писать пример
пример можно решить по виетто и это будет y=4 и y=6
если по виетто не умеешь то через дискриминант
5) мне лень писать пример
пример можно решить по виетто и это будет p=-10 и p=9
если по виетто не умеешь то через дискриминант
6) мне лень писать пример
7) мне лень писать пример
с дискриминанта решать
D= 324-4*81*1=324-324= 0- то есть p1 и p2 будут одинаковы
p1 и p2 =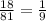
8) мне лень писать пример
пример можно решить по виетто и это будет y1=-8 и y2=19
если по виетто не умеешь то через дискриминант
9) мне лень писать пример
D= 121-4*5*2=121-40=81 - это 9 в квадрате
тогда x1=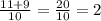
x2=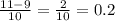
10) мне лень писать пример
с дискриминанта решать
D= 64-4*16*1=64-64= 0- то есть x1 и x2 будут одинаковы
x1 и x2 =