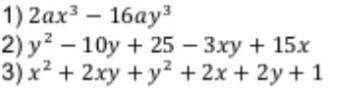
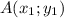 .
. 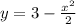 симметричен относительно оси
симметричен относительно оси 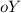 . Пересекающая ось
. Пересекающая ось 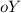 в точке
в точке 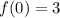 .
.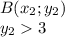 .
.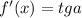 . Так как график симметричен , то угол образующие касательные
. Так как график симметричен , то угол образующие касательные 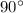 , ордината будет являться биссектрисой . Следовательно треугольник будет прямоугольным и равнобедренным.
, ордината будет являться биссектрисой . Следовательно треугольник будет прямоугольным и равнобедренным. 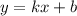
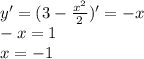 , так как
, так как 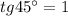
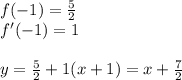
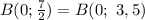
Объяснение:
вот если что 2у
это правильно