1) f(x) = x^2 - 6x + 5
D(f) = R
1) Знайдемо проміжки монотоності:
f`(x) = 2x - 6 = 2(x - 3)
f`(x) = 0
2(x - 3) = 0
x = 3
(дивись малюнок)
f(x) спадає якщо х ∈ (-∞; 3) і зростає якщо х ∈ (3; +∞)
2) знайдемо точки екстремума.
х(min) = 3 ⇒ y(min) = 3² - 6 * 3 +5 = 9 - 18 + 5 = -4
точки max не існеє.
2) f(x) = x^4 - 2x^2
D(f) = R
1) Знайдемо проміжки монотоності:
f`(x) = 4x³ - 4х = 4х(x² - 1) = 4х(х - 1)(х + 1)
f`(x) = 0
4х(х - 1)(х + 1) = 0
х = 0, х = 1, х = -1
(дивись малюнок)
f(x) спадає якщо х ∈ (-∞; -1) і (0; 1);
зростає якщо х ∈ (-1; 0) і (1; +∞)
2) знайдемо точки екстремума.
х(min) = -1 ⇒ y(min) = (-1)⁴ - 2 * (-1)² = 1 - 2 = -1
х(min) = 1 ⇒ y(min) = 1⁴ - 2 * 1² = 1 - 2 = -1
х(max) = 0 ⇒ y(max) = 0⁴ - 2 * 0² = 0
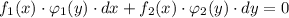
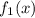и 
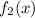зависят только от переменной "х" , а функци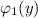и 
и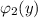 
зависят только от переменной "у" . Указывается на то, что диффер. уравнение допускает обособление (разделение) переменных только тогда, когда перед дифференциалами (dx и dy) стоят функции, являющиеся произведениями двух других функций, одна из которых зависит только от "х" , а вторая зависит только от "у" . 
. 
.
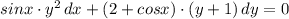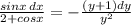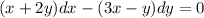, то переменные уже нельзя разделить, так как нельзя функции, стоящие перед dx и dy,представить в виде произведения 
.
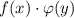(1/18)<x<32
Объяснение:
решение во вложении