1.
a)
x² + 4x + 10 ≥ 0
Рассмотрим функцию у = x² + 4x + 10.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 4x + 10 = 0
D = 16 - 40 = - 24 < 0
нулей нет, значит график не пересекает ось Ох.
Схематически график изображен на рис. 1.
у > 0 при x ∈ (- ∞; + ∞)
ответ: 2) Решением неравенства является вся числовая прямая.
b)
- x² + 10x - 25 > 0 | · (- 1)
x² - 10x + 25 < 0
Рассмотрим функцию у = x² - 10x + 25.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 10x + 25 = 0
(x - 5)² = 0
x = 5
Схематически график изображен на рис. 2.
у < 0 при x ∈ {∅}
ответ: 1) Неравенство не имеет решений.
c)
x² + 3x + 2 ≤ 0
Рассмотрим функцию у = x² + 3x + 2.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 3x + 2 = 0
D = 9 - 8 = 1
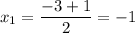
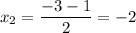
Схематически график изображен на рис. 3.
у ≤ 0 при x ∈ [- 2; - 1]
ответ: 4) Решением неравенства является закрытый промежуток.
d)
- x² + 4 < 0 | · (- 1)
x² - 4 > 0
Рассмотрим функцию у = x² - 4.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 4 = 0
x² = 4
x = ± 2
Схематически график изображен на рис. 4.
у > 0 при x ∈ (- ∞; - 2) ∪ (2; + ∞)
ответ: 6) Решением неравенства является объединение двух промежутков.
___________________________
2.
(x - a)(2x - 1)(x + b) > 0
x ∈(- 4; 1/2) ∪ (5; + ∞)
Решение неравенства показано на рис. 5.
Найдем нули функции у = (x - a)(2x - 1)(x + b).
(x - a)(2x - 1)(x + b) = 0
(x - a) = 0 или (2x - 1) = 0 или (x + b) = 0
x = a x = 1/2 x = - b
Из решения неравенства следует, что нулями являются числа - 4, 1/2 и 5. Значит
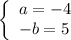 или
или 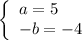
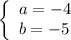 или
или 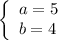
ответ: a = - 4, b = - 5 или a = 5, b = 4.
Объяснение:
1) 7÷100=0,07 (л) бензина расход на 1 км.
0,07*7000=490 (л) бензина расход за месяц.
490*30=14700 (руб) потратил таксист за месяц.
ответ: 14700 рублей.
2) 130*2=260 учебников привезли для двух курсов.
8*30=240 учебников помещается в один шкаф.
260÷240=1 (ост. 20) Один шкаф можно полностью заполнить новыми учебниками и 20 учебников останутся.
ответ: 1 шкаф.
3) 300÷45=6 (ост. 30) Имея 300 рублей можно купить 6 тюльпанов и ещё останется 30 рублей.
Т.к. 6 это четное число, то наибольшее нечетное количество тюльпанов в букете будет 5.
ответ: 5 тюльпанов.
4) 10÷100=0,1 (л) бензина расход на 1 км.
10000*0,1=1000 (л) бензина расход за этот месяц.
32*1000=32000 (руб) потратил таксист за этот месяц.
ответ: 32000 рублей.
5) 2 руб 40 коп = 2,4 руб.
80÷2,4=33 (ост. 0,8) Имея 80 рублей, можно купить 33 марки и ещё останется 0,8 руб или 80 коп.
ответ: 33 марки.
6) 10000÷360=27 (ост. 280) Имея 10000 рублей, можно купить 27 метров ткани и ещё останется 280 рублей.
ответ: 27 метров ткани.
7) 175÷3=58 (ост. 1) В 58 комнатах поселятся по 3 человека и ещё останется 1 человек. для которого то же нужна 1 комната.
58+1=59 (комн) Наименьшее количество комнат 59, для поселения 175 студентов.
ответ: 59 комнат.
8) 1852÷1000=1,852 (км) составляет 1 морская миля.
15*1,852=27,78 (км/ч) скорость корабля.
ответ: 27,78 км/ч.
Відповідь:
18 2/3
Пояснення:
Знайдіть суму нескінченної геометричної прогресії 28; -14; 7; ... .
b₁ = 28; b₂ = -14
q = b₂/b₁ = -14/28 = -1/2
S = b₁ / (1 - q) = 28 / (1 -(-1/2)) = 28/(1+1/2)=28/(3/2)=28*2/3=18 2/3