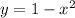
Это парабола, ветви которой направленны вниз, о чём говорит множитель -1 у 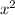 .
.
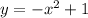
1 в данном случае обозначает, что график функции сдвинут вдоль оси Oy вверх на 1.
Т.е. отсюда видно, что функция, начинается выше оси Ох (принимая положительные значения) и в двух точках её пересекает своими ветвями, принимая отрицательные значения в дальнейшем. (Очевидно, что парабола может иметь не более двух точек пересечения с осью Ox, так что искать иных положительных значений не стоит)
Т.е. все множество положительных значений заключено между двумя корнями этой функции, а всё множество отрицательных, вне.
Корни видно из графика, это x_1 = 1 и x_2 = -1.
y` = 4x^3 +6x
y` = 3x^2-6x+1
y`= 6x+2
y`= 4x+ 1/ cos^2 x
y` = 5x^4-10x + cosx
y`= e^x + 1/x
y`= 1- 1/x
y`= -sinx +cos x
y`= 1/ (2*корень из х) - 1/ (х^2)
y`= 1/ (x ln 7) + 3
y`= 1/ (x ln 3) + 1/ (x ln 5)
y`= 5+2=7
y`= [(2x+5)(2-8x)+8(x^2+5x)] / (2-8x)^2 = (-8x^2+4x+10) / (2-8x)^2
y`= 6x
y`=9x^2-6
y`= cosx(1+cosx) - sinx(1+sinx)= cosx+cos^2 x-sinx-sin^2 x= cosx - sinx+ cos2x
y`= 1/( cos^2 x) - 2cosx
y`= 12x^2
y`= 12x^2-8
y`= 1/x * (x^2-1)+2x*lnx=(x^2-1) / x + 2x*lnx
y`= 4^x * ln4 * log4x + 4^x / (x*ln4)
(-∞;-3] ∪ [3;+∞)
Объяснение:
Общий ОДЗ функции состоит из двух неравенств: |x|-3≥0 и x²+0.16>=0.
Второе равенство верно для любого x, а первое выполняется только на открытых лучах от (-∞;-3] и [3;+∞) в силу определния модуля, как расстояния между х и нулем.