D (область определения) ∈ (+∞ : -∞)
Е (область значений) ∈ [11 ; -∞)
Объяснение:
область определения - это все значения х
область значений функции - это все у
По условию дано: f (x) = -х² + 6х + 2, высчитаем максимальный у (у данного графика есть у максимальное, так как ветви параболы направлен вниз), для этого нужно найти х вершины по формуле:
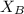 = -b/2a = -6/-2 = 3,
= -b/2a = -6/-2 = 3,
подставим это значение х в функцию и найдём у:
f (x) = -х² + 6х + 2 = -9 + 18 + 2 = 11
=> Е (область значений) ∈ [11 ; -∞)
в то время как D (область определения) ∈ (+∞ : -∞)
x^2+6x+9<0,
(x+3)^2<0,
нет решений; (x+3)^2≥0, x∈R
-x^2+6x-5≥0,
a=-1<0 - ветви параболы направлены вниз, часть параболы над осью Ох (≥0) расположена между корнями,
-x^2+6x-5=0,
x^2-6x+5=0,
по теореме Виета х_1=1, x_2=5,
1≤x≤5,
x∈[1;5]
x^2-4x+3≥0,
a=1>0 - ветви параболы направлены вверх,
x^2-4x+3=0,
x_1=1, x_2=3 - часть параболы над осью Ох расположена вне корней,
x≤1, x≥3,
x∈(-∞;1]U[3;+∞)
x^2-6x+8≤0,
a=1>0 - ветви параболы - вверх,
x^2-6x+8=0,
x_1=2, x_2=4 - часть параболы под осью Ох (≤0) расположена между корнями,
2≤x≤4,
x∈[2;4]
через 0,6 ч
Объяснение:
15/(85-60)=15/25=3/5=0,6 ч