Question

Решить уравнение: sqrt x+2=(sqrt 3-x)+1

Answer 1

x>=-2

x<=3

[-2;3]

x+2=3-x+1+2sqrt(3-x)=4-x+2sqrt(3-x)

2x-2=2sqrt(3-x)

x-1=sqrt(3-x)

x^2+1-2x=3-x

x^2-x-2=0

x1=-1

x2=2

ответ -1; 2

Answer 2

$\sqrt{x+2}=\sqrt{3-x}+1$

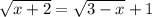
Для начала найдём ОДЗ, т.к. подкоренное выражение не может быть отрицательным, то

$\left \{ {{x+2\geq0} \atop {3-x\geq0} \right.$

$\left \{ {{x\geq-2} \atop {x\geq3} \right.$

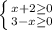
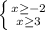
Общее решение: [-2; 3]

Теперь вернемся к решению уравнения.

Возведем левую и правую часть в квадрат

$x+2=3-x+2*\sqrt{3-x}+1$

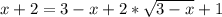
Приведем подобные слагаемые

$x+2=4-x+2\sqrt{3-x}$

$x+2-4+x=2\sqrt{3-x}$

$2x-2=2\sqrt{3-x}$

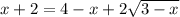
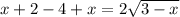
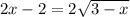
В левой части уравнения вынесем двойку за скобку

$2(x-1)=2\sqrt{3-x}$

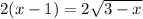
Сократим левую и правую часть уравнения на 2

$x-1=\sqrt{3-x}$

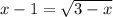
Опять возведеем обе части уравнения в квадрат

$x^{2}-2x+1=3-x$

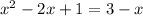
Перенесем все в одну часть и приведем подобные слагаемые

$x^{2}-x-2=0$

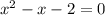
Решим квадратное уравнение

Найдём корни по теореме Виета

x1=2      x2=-1 (можно найти дискриминант, получатся эти же значения)

Связуем корни с ОДЗ, оба ответа входят в промежуторк [-2;3]

ответ: 2 и -1

 Если задание записано в виде: 

$\sqrt{x}+2=\sqrt{3-x}+1$

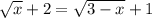
то ОДЗ:

{x>=0

{x<=3

 [0;3]

Перенсем двойку в правую часть

$\sqrt{x}=\sqrt{3-x}-1$

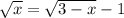
Возведем обе части в квадрат

$x=3-x2\sqrt{3-x}+1$

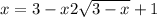
Приведем подобные слагаемые

$x=-x+4-2\sqrt{3-x}$

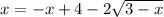
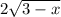
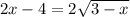
Перенесем в левую часть все, кроме $2\sqrt{3-x}$

$2x-4=2\sqrt{3-x}$

В левой части вынесем двойку за кобку

$2(x-2)=2\sqrt{3-x}$

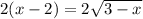
Сокращаем на 2

$x-2=\sqrt{3-x}$

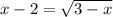
Возведем обе части в квадрат

$x^{2}-4x+4=3-x$

Перенсоим все в левую часть и приводим подобные

$x^{2}-4x+4-3+x=0$

$x^{2}-3x+1=0$

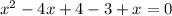
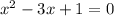
Решаем квадратное уравнение. Найдём дискриминант

D=9-4=5

$x_{1}=\frac{3+\sqrt{5}}{2}$

$x_{2}=\frac{3-\sqrt{5}}{2}$

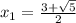
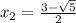
Согласуем корни с ОДЗ. Для этого найдем приблизительное значение корней

$x_{1}\approx2,6$

$x_{2}\approx0,4$

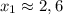
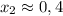
Оба корни входят в ОДЗ, поэтому оба корня являются ответом