S=6400м²
Пусть ширина равна х м,тогда длина равна (х+36) м.
Составим уравнение:
х(х+36)=6400
х²+36х-6400=0
D=1296+25600=164²
x₁=(-36-164)/2=-100---не удовлетворяет условию задачи.
x₂=(-36+164)/2=64м---ширина
Отсюда х+36=64+36=100м длина
ответ:64 м;100 м.
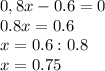
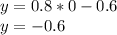
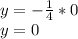
а) х² - х + 1/4
х может принимать любые действительные значения.
б) (х+1)/(х²+9) + 2х
Знаменатель дроби не должен равняться нулю.
Рассматриваем знаменатель х²+9 и видим, что он всегда больше нуля, поэтому опять:
х может принимать любые действительные значения.
в) 14\3х-6
Знаменатель дроби не должен равняться нулю.
Рассматриваем знаменатель 3х - 6 ≠ 0 ⇒ 3х ≠ 6 ⇒ х ≠ 2
х может принимать любые действительные значения, кроме х = 2
г) х²-3/(3-2х)(х+5)
Рассматриваем знаменатель
1) 3 - 2х ≠0 ⇒ -2х ≠ -3 ⇒ х ≠ 1,5
2) х+5 ≠ 0 ⇒ х ≠ -5
х может принимать любые действительные значения, кроме х = 1,5 и х = -5
д)х²+1/х(х+3)
Рассматриваем знаменатель
1) х ≠0
2) х+3 ≠ 0 ⇒ х ≠ -3
х может принимать любые действительные значения, кроме х = 0 и х = -3
е) 2х/(х-1)²·(х²-4)
Рассматриваем знаменатель
1) х - 1 ≠ 0 ⇒ х ≠ 1
2) х² - 4 ≠ 0 ⇒ х² ≠ 4 ⇒ х ≠ -2 и х ≠ 2
х может принимать любые действительные значения, кроме х = 1, х = -2 и х = 2
S=ab, где a - длина, а b - ширина
Возьмём ширину за х
Тогда длина будет х+36
Составим уравнение:
x*(x+36)=6400
x^2+36x-6400=0
D=1296+25600=26896
Sqrt(D)=164
x=(-36+164)/2=64 (ширина)
x=-200/2=-100 (не годится, ширина отрицательной быть не может)
Тогда х+36=64+36=100 (длина)
ответ: Длина поля=100 м, а ширина - 64 м.