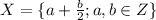
Если взять a=0, b=1, то получается элемент 1/2, квадрат которого равен 1/4 и поэтому не лежит в X. Таким образом, обычное умножение выводит из этого множества, и поэтому не имеет права претендовать на гордое название "алгебраической операции". После этого смешно говорить про ассоциативность (а она бы была, если бы операция не выводила бы из X), про коммутативность (а она бы... - см. текст выше), наличие нейтрального элемента (см. выше). Не знаю, какие элементы Вы называете симметричными, обычно говорят про обратные, но здесь с обратными проблема. В общем, говорить о группе не приходится, как и о группоиде, полугруппе или моноиде
Y-X=7
X*Y=-12
Из верхнего уравнения выводим Y:
Y=7+Х
Подставляем Y в нижнее уравнение и получаем:
Х*(7+Х)=-12
Открываем скобки и переносим -12 в левую часть для того что бы привести уравнение к квадратному:
Х^2+7*X+12=0
Есть методика решения квадратных уравнений через дискриминант. Если дискриминант больше нуля - то квадратное уравнение имеет два решения.
Формулы нахождения решения в ссылке ниже (там же и калькулятор)
х1=-3
х2=-4
Подставляем х1 во второе уравнение:
-3*y=-12
y1=-12/-3=4
Подставляем х2 во второе уравнение:
-4*y=-12
y2=-12/-4=3