10/25-x^2 - 1/5+x - x/x-5 = 0
По формулам сокращенного умножения (а^2 - в^2) = (а + в)(а - в)
10/(5-х)(5+х) - 1/(5+x) + x/(5-х) = 0 (здесь поменяли знак на +, и дробь изменилась)
Общий знаменатель (5-х)(5+х)
Получаем в числителе Знаменатель
10-5+х+5х+х^2 = 0 (5-х)(5+х) не равно 0
х^2+6х+5 = 0 5-х не равно 0, х не равен 5
Д = 36-4*1*5 = 36-20 = 16 5+х не равно 0, х не равен -5
х1 = (-6+4) / 2 = -1
х2 = (-6-4) / 2 = -5 не берем
ответ: х = -1
a)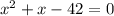 
Ищем дискриминант:
D=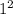
-4*1*(-42)=1-4*(-42)=1-(-4*42)=1-(-168)=1+168=169;
Дискриминант больше 0, уравнение имеет 2 корня: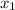
=
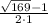=(13-1)/2=12/2=6;
= 
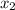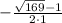=(13-1)/2=12/2=6 =(-13-1)/2=-14/2=-7.
б)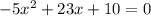 
Ищем дискриминант:
D=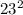
-4*(-5)*10=529-4*(-5)*10=529-(-4*5)*10=529-(-20)*10=529-(-20*10)=529-(-200)=529+200=729;
Дискриминант больше 0, уравнение имеет 2 корня: =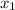 
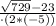=(27-23)/(2*(-5))=4/(2*(-5))=4/(-2*5)=4/(-10)=-4/10=-0.4;
= 
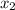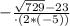=-50/(2*(-5))=-50/(-2*5)=-50/(-10)=-(-50/10)=-(-5)=5.
в)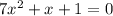 
Ищем дискриминант:
D=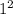-4*7*1=1-4*7=1-28=-27;
Дискриминант меньше 0, уравнение не имеет корней.
г)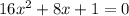 
Ищем дискриминант:
D=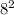 
-4*16*1=64-4*16=64-64=0;
Дискриминант равен 0, уравнение имеет 1 корень:
X=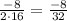
=-0.25
Если условие правильно списано из учебника и в учебнике нет опечатки, решение следующее
Возведём в квадрат левую часть, получим
A^2 + 4*a*A + 4*a^2 = B + 4*a*18*b + 4*a^2
Так как это тождество, обязательно одновременно выполняются 2 равенства
A^2 = B
A = 18*b, то есть A^2 = 18^2*b^2( =В), поэтому
A*B = 18*b*18^2*b^2 = 18^3*b^3.
Это и всё решение. b выступает свободным параметром, то есть есть серия чисел, которые удовлетворяют поставленному условию, а именно,
b=0 A*B=0
b=+-1 A*B=18^3*(+-1)^3 = +-5832
b=+-2 A*B=18^3*(+-2)^3 = 5832*(+-8) =+-46656, и т.д.
Вот такое "некрасивое" параметрическое решение получилось. Не нравится оно мне, всё же или в учебнике опечатка или Авторы задачи её составляли, не заботясь об эстетическом наслаждении решающих, лишь бы чего написать. Увы, вот такое моё впечатление.