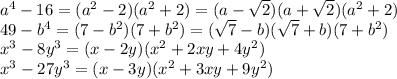
В результате выделения полных квадратов получаем:
-4(x - 2)² + 25(y + 2)² = 100
Разделим все выражение на 100 :
(-1/25)(x - 2)² + (1/4)(y + 2)² = 1.
Параметры кривой.
Данное уравнение определяет гиперболу с центром в точке:
C(2; -2) и полуосями:
a = 5 (мнимая полуось); b = 2 (действительная полуось) .
Вершины:(2; 0) и (2; -4).
Найдем координаты ее фокусов: F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами
Определим параметр c: c² = a² + b² = 25 + 4 = 29
Тогда эксцентриситет будет равен: e = c/a = √29/5.
Асимптотами гиперболы будут прямые: y + 2 = +-(2/5))x - 2)
Директрисами гиперболы будут прямые: (x - 2) = +-(25/√29).

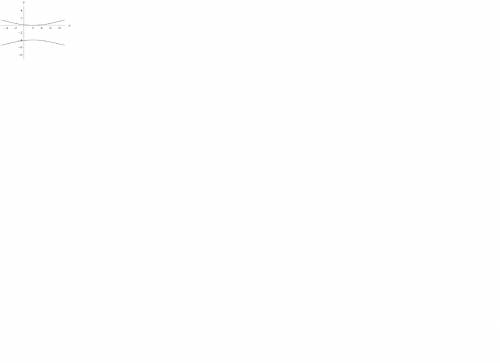
Запишем уравнение кривой в виде -4*(x²-4*x)+25*(y²+4*y)-16=0, или -4*[(x-2)²-4]+25*[(y+2)²-4]-16=0, или -4*(x-2)²+25*(y+2)²=100, или -(x-2)²/25+(y+2)²/4=1. Это есть уравнение гиперболы с центром симметрии в точке (2;-2), вещественной полуосью a=√25=5 и мнимой полуосью b=√4=2. Вершины гиперболы в данном случае лежат на прямой x=2, параллельной оси ординат. Одни из вершин имеет координаты (2;3), другая - координаты (2;-7). Асимптоты гиперболы задаются уравнениями y-y0=b/a*(x-x0) и y-y0=-b/a*(x-x0), где x0 и y0 - координаты центра симметрии. В нашем случае x0=2, y0=-2, a=5,b=2, поэтому уравнения асимптот принимают вид: y+2=2/5*(x-2) и y+2=-2/5*(x-2).