Ну 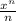 указывает на то, что надо бы производную брать для исследования этой функции, ибо она красивая получается.
указывает на то, что надо бы производную брать для исследования этой функции, ибо она красивая получается.
Далее, для исследования исходной функции на возрастание/убывание необходимо найти нули производной, то есть 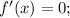
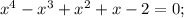
Сумма коэффициентов в уравнении равно 0, значит, x=1 - корень
Попробуем разложить выражение, заранее зная корень.
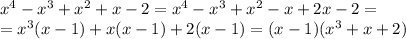
Теперь нужно проанализировать правую скобку 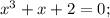
Сумма коэффициентов при четных (2) и нечетных (1+1=2) степенях равна, значит, x=-1 - корень. 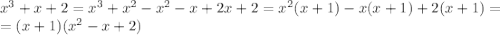
Осталась последняя скобка в разложении, найдем дискриминант уравнения
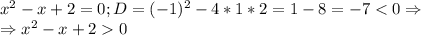 при любых х.
при любых х.
Итоговое разложение 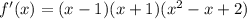
Нули производной известны, это 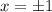
Везде при х коэффициент равен 1 (у правой скобки нет нулей, её мы считаем просто каким-то положительным числом), значит, в самом правом промежутке "+", а дальше чередование.
Имеем при 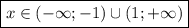 возрастание
возрастание  , а при
, а при 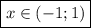 убывание
убывание  ,
,
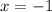 - точка локального максимума,
- точка локального максимума,
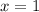 - точка локального минимума.
- точка локального минимума.
Убывание должно быть на интервале 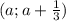 , поэтому если параметр захватит точки экстремума - ничего страшного, интервал как раз не включает концы.
, поэтому если параметр захватит точки экстремума - ничего страшного, интервал как раз не включает концы.
С одной стороны, 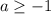 , как раз при
, как раз при  убывание на
убывание на 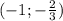 выполняется.
выполняется.
С другой стороны,  , при
, при 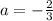 убывание продолжается вплоть до x=1, не включая эту точку.
убывание продолжается вплоть до x=1, не включая эту точку.
Объединяя наши условия, получаем ![$1\leq a\leq \frac{2}{3} \Rightarrow a\in[1;\frac{2}{3}]](/tpl/images/0725/1569/fb3d8.png)
ответ: ![\boxed {a\in[1;\frac{2}{3}]}](/tpl/images/0725/1569/80e87.png)
Пусть n - первое число, тогда n+1 -второе, а n+2 - третье.
n² - квадрат меньшего числа, а (n+1)(n+2) - произведение двух других чисел.
Т. к. n² < (n+1)(n+2) на 17, составим уравнение:
(n+1)(n+2) - n² = 17
2 этап. Решение математической задачи.
(n+1)(n+2) - n² = 17
n²+2n+n+2-n² = 17
2n+n=17-2
3n=15
n=15:3
n=5; n+1=5+1=6; n+2=5+2=7
3 этап. Анализ результата.
5 - первое число, 6 - второе число, 7 - третье число.
5, 6, 7 - последовательные натуральные числа.
ответ: 5, 6, 7
Проверка:
6*7-5² = 17
42-25 = 17
17 = 17