Question

Решить: 1) вычислить предел lim=корень(9n^2+8n-6) /(4n+8), x⇒∞ 2)найдите вертикальные асимптоты x=a графика функции f(х)= (-3x^3+2x^2+3x) / (x^2-2x-15). в ответе укажите сумму всевозможных значений а. 3)для функции f(x)=(7x^2+4x-5)/ x^2 найдите точку
локального максимума

Answer 1

1) $\lim_{x \to \infty} \frac{\sqrt{9x^2-8x-6}}{4x+8}=\lim_{x \to \infty} \frac{x\sqrt{9-\frac{8}{x}-\frac{6}{x^2}}}{x(4+\frac{8}{x})}=\frac{3}{4}$

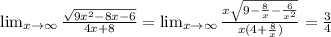
2) x²-2x-15≠0 (x₁=-3, x₂=5)

Функция определена при x∈(-∞, -3)U(-3, 5)U(5, +∞)

Односторонние пределы можно уже не находить, x=-3, x=5 - вертикальные асимптоты.

$\lim_{x \to \infty} \frac{-3x^3+2x^2+3x}{x(x^2-2x+15)}=\lim_{x \to \infty} \frac{x^3(-3+\frac{2}{x}+\frac{3}{x^2})}{x^3(1-\frac{2}{x}+\frac{15}{x^2})}=-3$

k=-3

$\lim_{x \to \infty} \frac{-3x^3+2x^2+3x}{x^2-2x+15}+3x=\lim_{x \to \infty} \frac{-4x^2+48x}{x^2-2x+15}=-4$

y=-3x-4 - наклонная асимптота

3) $f'(x) = \frac{-4x+10}{x^3}$

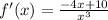
Найдем критические точки

x = 5/2, x=0

x=5/2 - точка локального максимума (производная меняет свой знак в этой области)