1) Будем смотреть по четвертям: в 1-й четверти и синус, и тангенс положительны. но при одинаковых углах синус меньше, чем тангенс ( смотри на ед окружности) во 2- й четверти синус положителен, а тангенс с минусом ( наше неравенство выполняется) Значит, ответ: (π/2; π) в 3-й четверти синус с минусом, а тангенс с плюсом ( не подходит) в 4-й четверти снова синус положителен, а тангенс отрицателен. (наше неравенство выполняется)значит, ответ: (3π/2; 2π) 2) Решаем как квадратное: D = 1 -4*4*(-5) = 81 а) Cosx = (-1 +9)/8 = 1, x = 2πk, k ∈Z б) Cosx = (-1 -9)/8 =-5/4 нет решения 3) arcSin(Sin5) = 5
1)Центр окружности, находится в середине диаметра. Значит нужно найти середину AB. Для этого воспользуемся формулой нахождения середины отрезка через координаты его крайних точек. т.O(; ), где т.О - центр окружности, (;) координаты точки А, (;) - координаты точки В. т.О(;), т.е. т.О(4;3). 2) Для того, чтоб найти радиус, нужно найти расстояние от центра окружности до точки А. Воспользуемся формулой нахождения длины отрезка через координаты его крайних точек. OА=, где ОА - радиус, (;) - координаты точки А, (;) - координаты точки О. ОА===√17 ответ: О(4;3), ОА=√17
Объяснение:
Варіант 1:
1)2 =32
=32
x=+4 або х=-4
2)5 +10x=0
+10x=0
5x(x+10)=0
5x=0 або х+10=0
х=0 або х=-10
3) -8х-9=0
-8х-9=0
D=64-4*1*(-9)=100
x1=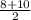 =9
=9
x2=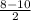 =-1
=-1
4)3 -8x-3=0
-8x-3=0
D=64-4*3*(-3)=100
x1=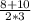 =3
=3
x2=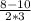 =-
=-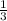
5) -4x+9=0
-4x+9=0
D=16-4*1*9=-20 (дискримінант відємний тому коренів немає)
порожня множина
Варіант 2:
1)-3 +27=0
+27=0
-3( -9)=0
-9)=0
х=3 або х=-3
2)7 -14х=0
-14х=0
7х(х-2)=0
х=0 або х=2
3) -8х+7=0
-8х+7=0
D=64-4*1*7=36
x1=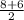 =7
=7
x2=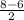 =1
=1
4)2 -3x-2=0
-3x-2=0
D=9-4*2*(-2)=25
x1=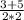 =2
=2
x2=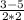 =-0.5
=-0.5
5) -6x+9=0
-6x+9=0
D=36-4*1*9=0 (отже один корінь)
x=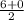 =3
=3