На 1 месте может быть любая цифра от 1 до 9, то есть 9 вариантов.
Н 2, 3, 4 и 5 месте - любая от 0 до 9, то есть по 10 вариантов.
Всего 9*10*10*10*10 = 90 000 вариантов.
а) Все цифры разные. На 1 месте может быть любая цифра от 1 до 9 - 9 вариантов.
На 2 месте может быть 0 и любая из 8 других цифр, но не та, которая на 1 месте. - 9 вариантов.
На 3 месте может быть любая из 8 оставшихся цифр. На 4 - любая из 7, на 5 - любая из 6.
Всего 9*9*8*7*6 = 27216 вариантов. Вероятность равна 27216/90 000 = 0,3024
б) Все цифры одинаковые - таких вариантов всего 9, от 11111 до 99999. Вер-сть 1/10 000 = 0,0001
в) Все цифры нечетные На каждом месте может быть одна из 5 цифр - 1,3,5,7,9.
Всего 5*5*5*5*5 = 3125 вариантов. Вероятность равна 3125/90 000 = 0,03472
2)Из обеих урн достают по одному шару.
Какова вероятность, что они будут одного цвета?
5/24*10/24 + 11/24*8/24 + 8/24*6*24 = 31/96 = 32.3%
ответ : 32.3%
3) ПО ОПРЕДЕЛЕНИЮ вероятность это отношение числа нужных вариантов к общему числу вариантов (какого-то события). То есть 2*9!/10! = 1/5;
4)Где-то 50 процентов
Дальше я хз
Объяснение:
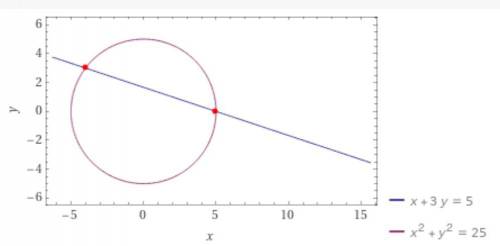
Дана система уравнений :
{х+ Зу = 5, это прямая линия у = (-1/3)х + (5/3)
{х² + y² = 25, это окружность с центром в начале координат и радиусом 5.
Общая схема графического решения - начертить окружность и провести линию через 2 точки: х = 0, у = (5/3) и у = 0, х = 5.
Точки пересечения линий и есть решение.
Можно аналитически проверить его правильность.
{х+ Зу = 5, х = 5 - 3у подставить во второе уравнение.
{х² +y² = 25. (5 - 3у)² + у² = 25.
25 - 30у + 9у² + у² = 25. Решаем квадратное уравнение:
10у² - 30у = 0 или 10у(у - 3) = 0.
Получили 2 корня: у1 = 0 и у2 = 3, отсюда соответствующие координаты по оси Ох равны:
х1 = 5, х2 = -4.
х=10,6
аллалалаллалклклклклклал