Решение.
Поскольку 3000 и 1980 делятся на 60, Володя сможет снять лишь сумму, кратную 60 рублям. Максимальное число, кратное 60 и не превосходящее 5000, - это 4980.
Докажем, что снять 4980 рублей возможно. Произведем следующие операции: 5000-3000=2000, 2000+1980=3980, 3980-3000=980, 980+1980=2960, 2960+1980=4940. Сумма, лежащая на счете, уменьшилась на 60 рублей.
Проделав аналогичную процедуру 16 раз, Петя снимет 960 рублей. Затем он может снять 3000, положить 1980 и снова снять 3000. В результате у него будет 4980 рублей.
Заметим, что в условии не сказано, что все числа разные. Будем считать, что числа записаны в порядке возрастания:
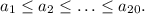Условие, что сумма любых пяти из них не меньше 117, равносильно тому, что сумма наименьших пяти не меньше 117:
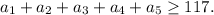Чтобы сделать сумму всех чисел как можно меньше, надо сделать 
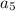как можно меньше и взять все числа с большими номерами равными 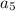. Чтобы упростить рассуждение, приведу нужный набор чисел и докажу, что любой другой даст большую сумму:
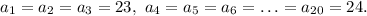
Сумма первых пяти чисел равна 117, сумма всех равна 477. Сумма первых пяти тем самым минимально возможная, поэтому попытка сделать сумму всех чисел меньше приводит к тому, что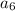 
должен стать меньше, чем 24, а тогда и пятый член окажется меньше 24, а тогда сумма первых пяти окажется не больше, чем 
.
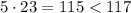ответ: 477
АС=4
Диагонали квадрата равны, в точке пересечения делятся пополам и взаимно перпендикулярны, поэтому,
Треуг.ВОС
— равнобедренный и прямоугольный. Достроив его до прямоугольника ВОСК, получим квадрат с диагональю, равной стороне данного квадрата. Тогда его сторона
Ос=1/2АС=2м
ответ:
2м