x2=3*2^2-1/4*2^2+1=12-1/16+1=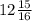
x100=3*100^2-1/4*100^2+1=30000+1-1/40000=30000\frac{39999}{40000}
последовательность является строго монотонной возрастающей, но не имеет предела, так что это доказать невозможно. Строго монотонна она потому что при неограниченном возрастании n первое слагаемое в рекурентной формуле неограниченно возрастает, а второе слагаемое постоянно убывает, в то время как 3е остается неизменным. То есть на каждом новом шаге мы все из большего вычитаем все меньшее. А предела не имеет так как послеовательноть не является ограниченной, это раз, и не выполняется критерий коши для сходимости последовательности, т.е. она не является фундаментальной, это 2
Забыл: Xn+1=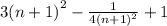
I. Надеюсь, что под корнем всё выражение)
• Перепишем исходную функцию:
y = 4√(x² - 8x + 15)
D (y) - ?
• Выражение под корнем должно быть неотрицательным, т.е. получаем следующее неравенство:
x² - 8x + 15 ≥ 0
• Вводим функцию:
ƒ (x) = x² - 8x + 15 , D (ƒ) = ℝ
• График парабола, ветви вверх
• Ищем нули функции:
x² - 8x + 15 = 0
По теореме, обратной теореме Виета:
x(1) = 5 и x(2) = 3
• Строим числовую ось, отмечаем точки и учитывая направление ветвей параболы ищем промежутки знакопостоянства
• Получается, что ƒ (x) ≥ 0 на: ( - ♾ ; 3] ⋃ [5 ; + ♾ )
⇒ D (y) : ( - ♾ ; 3] ⋃ [5 ; + ♾ )
ответ: ( - ♾ ; 3] ⋃ [5 ; + ♾ )
II. Но если под корнем только был x, то гораздо проще:
y = 4√x² - 8x + 15
D (y) - ?
x² ≥ 0
А квадрат любого действительного числа всегда будет неотрицательным, ⇒ D (y) = ℝ
ответ : ℝ