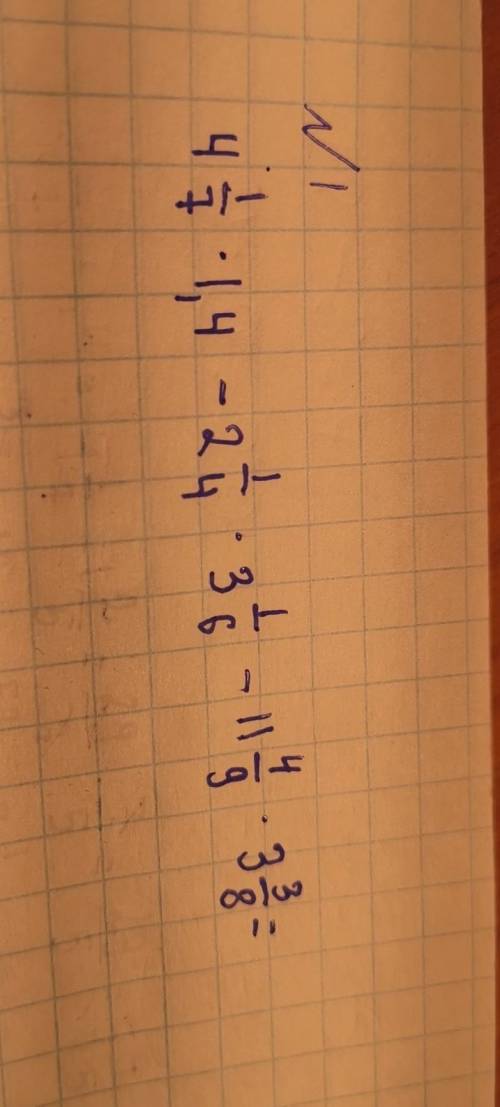

1) Выразим y из первого уравнения:
y = 1 - ax
Подставим y во второе уравнение:
4x - 2(1 - ax) = a
4x - 2 + 2ax = a
2(2x-1) + a(2x-1) = 0
(a+2)(2x-1) = 0
При a = -2 уравнение всегда равно нулю, то есть верно. Поэтому при а = -2 имеется бесконечное количество решений.
2) Делаем тоже, что и в первом:
y = (3-ax)/2
8x+ a(3-ax)/2 = a+2
8x + (3a - a^2 * x)/2 = a+2 | * 2
16x + 3a - a^2 * x = 2a + 4
-a^2 * x + a + 16x - 4 = 0
x(16 - a^2) + (a-4) = 0
x(4-a)(4+a) - (4-a) = 0
(4-a)(x(4+a) - 1) = 0
(4-a)(4x + ax - 1) = 0 (1)
Для того, чтобы а давало одно решение системе, необходимо, во-первых, чтобы а не было равно 4(тогда повторится история первого примера, будет бесконечно корней), а во-вторых, при любом а, отличном от четырёх и от минус четырёх, у уравнения (1) всегда будет один корень, потому что а - это простое число, (4-а) - тоже, а 4х + ах - 1 превращается в обычное линейное уравнение, которое имеет только один корень. В случае, когда а = -4, то уравнение превращается вот во что: (4+4)(4х - 4х - 1) = 0
8*(-1) = 0 , что неверно.
Значит, значение параметра может быть любым числом, кроме 4 и -4. =)
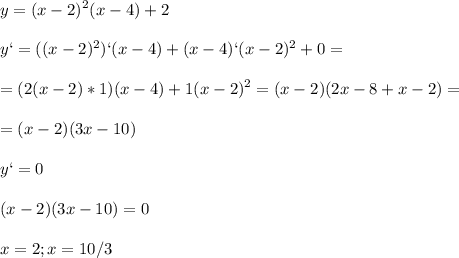
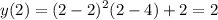
799:20
Объяснение:
Сначала нужно всё перевести в неправильные дроби, потом сократить некоторые числа, привести к общему знаменателю и получится ответ