1)((a⁷ - 8b⁴)(8b⁴ + a⁷) + 63b⁸)² - a¹⁴(+2b⁸ + a¹⁴) =
= (a¹⁴ - 64b⁸ + 63b⁸)² - 2a¹⁴b⁸ - a²⁸ = (a¹⁴ - b⁸)² - 2a¹⁴b⁸ - a²⁸ =
= a²⁸ - 2a¹⁴b⁸ + b¹⁶ - 2a¹⁴b⁸ - a²⁸ = b¹⁶
b¹⁶ = b¹⁶
2) b²⁴ - (82c¹⁰ + (b⁶ - 9c⁵)(9c⁵ + b⁶))² + c²⁰ = b²⁴ - (82c¹⁰ + b¹² - 81c¹⁰)² + c²⁰ =
= b²⁴ - (c¹⁰ + b¹²)² + c²⁰ = b²⁴ - c²⁰ - 2c¹⁰b¹² - b²⁴ + c²⁰ = -2c¹⁰b¹²
-2c¹⁰b¹² = - 2c¹⁰b¹²
3)(x³ - 9y⁴)² - (x³ + 9y⁴)² + 36x³(y⁴ - x) = (x³ - 9y⁴ - x³ - 9y⁴)(x³ - 9y⁴ + x³ + 9y⁴)+ 36x³y⁴ - 36x⁴ = - 18y⁴ * 2x³ + 36x³y⁴ - 36x⁴ = - 36x³y + 36x³y⁴ - 36x⁴ =
= - 36x⁴
- 36x⁴ = - 36x⁴
4) 0,5z⁴(40zt² - 5) - (z⁵ + 10t²)² + (10t² - z⁵)² =
= 20z⁵t² - 2,5z⁴ - z¹⁰ - 20z⁵t² - 100t⁴ + 100t⁴ - 20z⁵t² + z¹⁰ = -2,5z⁴ - 20z⁵t²
- 2,5z⁴ - 20z⁵t² = - 2,5z⁴ - 20z⁵t²
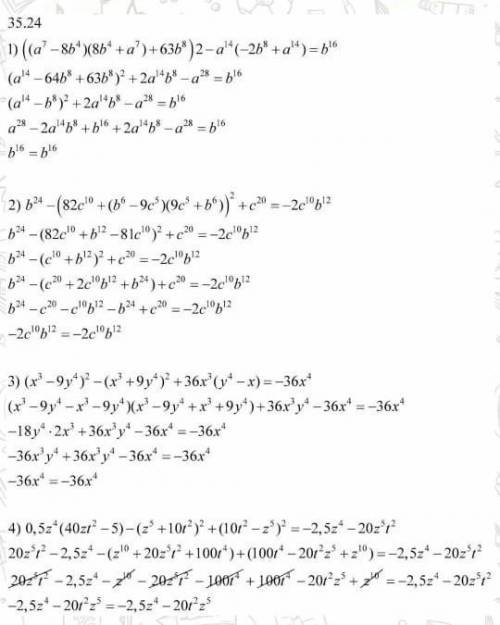
b = AD = AE + EF +FD
Мы знаем, что:
AE = FD;
EF = BC = 7 см.
Получаем:
b = AD = 2 * AE + BC (2)
Найдем длину отрезка AE. Рассмотрим прямоугольный треугольник ABE. Мы знаем, что угол А = 60 градусов следовательно угол B будет равен 30 градусов. Из свойств прямоугольного треугольника мы знаем, что катет лежащий напротив угла в 30 градусов равен половине гипотенузы. То есть в нашем случае:
AE = 1/2 * AB
Из условия мы знаем, что AB = 8 см. Тогда:
AE = 1/2 * AB = 1/2 * 8 = 4 см.
Вернемся к формуле (2):
b = AD = 2 * AE + BC = 2*4 + 7 = 8 + 7 = 15 см
Средняя линия трапеции (1):
m = (a + b) / 2 = (7 + 15) / 2 = 22 / 2 = 11 см
Объяснение: