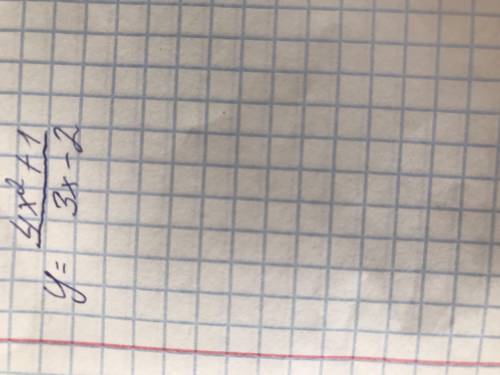
![y=\dfrac{4x^2+1}{3x-2}\\\\\\1)\ vertikalnue:\ \lim\limits_{x \to \frac{2}{3}}\dfrac{4x^2+1}{3x-2}=\Big[\dfrac{4\cdot \frac{4}{9}+1}{0}\ \Big]=\infty \ \ \Rightarrow \ \ \ \boxed {\ x=\dfrac{2}{3}\ }\\\\\\2)\ \ gorizontalnue:\ \ y=kx+b\\\\k=\lim\limits_{x \to \infty}\dfrac{f(x)}{x}=\lim\limits_{x \to \infty}\dfrac{4x^2+1}{3x^2-2x}=\lim\limits_{x \to \infty}\dfrac{4x^2}{3x^2}=\dfrac{4}{3}\\\\\\b=\lim\limits_{x \to \infty}(f(x)-kx)=\lim\limits_{x \to \infty}\Big(\dfrac{4x^2+1}{3x-2}-\dfrac{4x}{3}\Big)=](/tpl/images/1763/3002/e01cf.png)
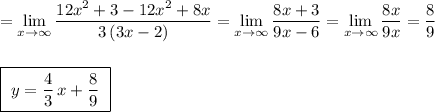
Х² + 9х = 0
I.Рациональный решения.
Вынести общий множитель за скобку:
х * (х + 9 ) = 0
Произведение = 0 , если один из множителей =0.
х₁= 0
х + 9=0
х₂= -9
II. Решение через дискриминант [ D= b² -4ac ]
Стандартный вид квадратного уравнения:
х² + 9х + 0 =0
а = 1 ; b= 9 ; с = 0
D = 9² - 4*1*0 = 9²
D>0 - два корня уравнения [ х₁,₂ = (-b ⁺₋ √D)/2a ) ]
х₁ = ( - 9 + √9²) /(2*1) = (-9 + 9)/2 = 0/2 = 0
x₂ = ( - 9 - √9²) /(2*1) = (-9 - 9)/2 = -18/2 = - 9
ответ: ( - 9 ; 0 ) .
Объяснение:
1)2(3x+7)-8(x+3)<_3
6x"+14 - 8x -24 -3 <_0
-2x<_13
x>_ - 6,5 отмечаем на координатной прямой ,точка будет выколотой и [ -6,5. +бесконечность)
2)-3x^2 +8x + 3=0
D = 64- 4*(-3)*3= 64+ 36=100=10^2
x1= -8 +10 / -6 = -2/6=-1/3
x2=-8 - 10 /-6 = 3
OTVET : -1/3 ; 3
3)4x^2 - 4x - 15 <0
D= 16-4*4*(-15) = 16+ 240= 256= 16^2
x1= 4+16 / 8= 20/8=5/4
x2=4-16/ 8= -12/16 = -3/4
4)8+2x-6 = 4x+7
-2x = 5
x=-2,5
5) 5x +4 _> 2
3-2x <_ 4
5x _> -2
-2x<_1
x_>-2/5
x>_-1/2