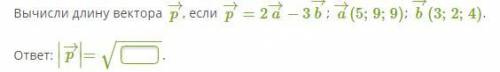


Объяснение:
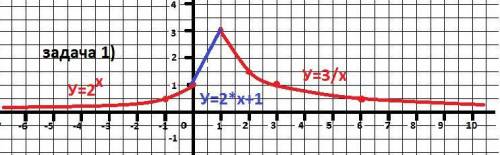
Задача 1) - рисунок к задаче в приложении.
При х=0 обе первых части графика совпадают в точке (0;1)
А третья функция: у = 3/х при х=1 равна
у(3) = 3/3 = 1.
Задача сводится провести прямую через две точки А(0;1) и В(1;3)
ДАНО: А(0;1), В(1;3)
НАЙТИ: Y = k*x + b
РЕШЕНИЕ
1) k = ΔY/ΔX = (Аy-Вy)/(Аx-Вx)=(1-(3))/(0-(1))=2 - коэффициент наклона прямой
2) b=Аy-k*Аx=1-(2)*0= 1- сдвиг по оси ОУ
Уравнение Y(АВ) = 2*x+1 - функция на втором участке.
ОТВЕТ: а = 2 - коэффициент.
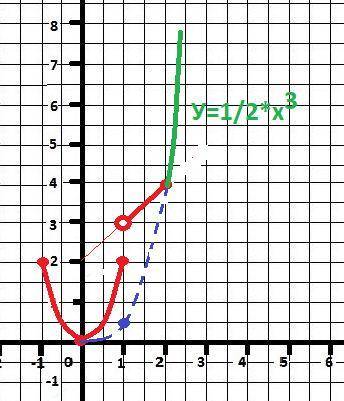
Задача 2) - рисунок в приложении.
При х = 2 на втором участке у = х + 2 = 4.
Задача сводится найти решение
y(2) = a*x³ = a*2³ = a*8 = 4
a = 4/8 = 0.5 = а - коэффициент - ответ.
Найдём координаты вектора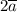 . Для этого все координаты вектора
. Для этого все координаты вектора 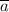 нужно умножить на 2:
нужно умножить на 2:
По такому же принципу найдём координаты вектора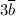 :
:
Чтобы найти координаты вектора , вычтем соответствующие координаты:
, вычтем соответствующие координаты:
Длина произвольного вектора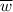 вычисляется по формуле
вычисляется по формуле 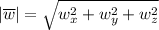 :
:
ответ: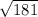 .
.
***
Координаты середины отрезка есть среднее арифметическое координат конца отрезка:
***
По условию точка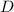 делит сторону
делит сторону 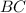 пополам (и так же с двумя другими точками). Найдём координаты точки
пополам (и так же с двумя другими точками). Найдём координаты точки
Расстояние между точками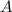 и
и 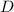 (т. е. длина медианы) равно:
(т. е. длина медианы) равно:
То есть .
.
То же самое проделаем с двумя другими медианами:
- - - - - - -
***
Если что-либо будет непонятно — спрашивайте.