Найдем вероятность того, что у определенного работника взятая деталь стандартная (как отношение соответствующего числа стандартных деталей к общему числу деталей):
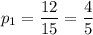
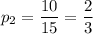
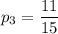
Поскольку события выбора по одной детали у каждого из работников независимы, то вероятность выбора у всех рабочих стандартных деталей определяется произведением вероятностей:
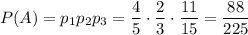
Найдем вероятности выбора нестандартных деталей у каждого работника:
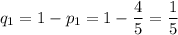
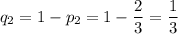
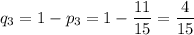
Одна стандартная деталь может быть выбрана только у первого работника, только у второго или только у третьего. Вероятность каждого из событий находится как произведение одной вероятности выбора стандартной детали на две другие вероятности выбора нестандартных деталей. Поскольку такие события несовместны, то полученные вероятности необходимо сложить.
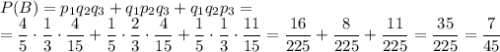
ответ: А) 88/225; Б) 7/45
а) Сумма равна 1, это одна возможная комбинация: {0} {1}, поэтому:
б) Сумма равная 2, это ({0};{2}), можно было бы составить другой комбинацией, но у нас нет двух карточек с единицами, поэтому вероятность так же равна:
в) Сумма равна 3, это ({0};{3}) или ({1};{2})
Вероятность равна:
г) Сумма равна 6, это ({0};{6}) ({1};{5}) ({2};{4})
Вероятность равна:
д) Сумма равна 9, это: ({0};{9}) ({1};{8}) ({2};{7}) ({3};{6}) ({4};{5})
Вероятность равна:
Таким образом, можно заметить, что вероятность зависит только от кол-ва составлений данного числа другими числами с карточек.