пусть а - сторона основания, а l - апофема, тогда формула площади поверхности конуса равна 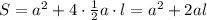
Подставим вместо а и S их значения и найдем апофему l
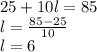
Через апофему проведем сечение пирамиды. В сечении получаем равнобедренный треугольник, основание которого равно стороне а=5, а боковые стороны апофеме l=6. Угол между боковой стороной треугольника и его основанием и есть угол наклона боковой грани пирамиды к плоскости основания. Найдем его, проведем высоту в равнобедренном треугольнике к его основанию. Высота равнобедренного треугольника, проведенная к основанию является так же его биссектрисо и медианой. Поэтому она делит равнобедренный треугольник на два равных прямоугольных треугольника. Найдем косинус искомого угла из прямоугольного треугольника.
Cos A=2,5/6=25/60=5/12 Отсюда следует, что угол наклона боковой грани к плоскости основания пирамиды равен arccos (5/12)
Відповідь:
-х³-х²-8х-22=0
Пояснення:
-(х²-2)(х-2)-5(х+1)² = 2(3-х²)+7
-(х³-2х²-2х+4)-5(х²+2х+1) = 6-2х²+7
-х³+2х²+2х-4-5х²-10х-5 = 6-2х²+7
-х³+2х²+2х-4-5х²-10х-5-6+2х²-7 = 0
-х³-х²-8х-22 = 0
Якщо вираз ×(-1) у нас вийде:
х³+х²+8х+22 = 0