1. Решите уравнение: 1) 5x2 − 10 = 0; 3) x2 + 6x − 7 = 0; 5) x2 − 3x + 1 = 0;
2) 3x2 + 4x = 0; 4) 3x2 + 7x + 2 = 0; 6) x2 − x + 3 = 0.
2. Составьте приведённое квадратное уравнение, сумма корней которого равна числу 6, а произведение — числу 4.
3. Одна из сторон прямоугольника на 7 см больше другой. Найдите стороны прямоугольника, если его площадь равна 44 см2.
4. Число −6 является корнем уравнения 2x2 + bx − 6 = 0. Найдите второй корень уравнения и значение b.
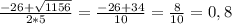

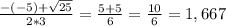

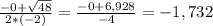
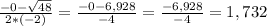
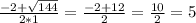
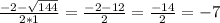
x2 + 4x + 8 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 42 - 4·1·8 = 16 - 32 = -16
Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
4x2 - 12x + 9 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-12)2 - 4·4·9 = 144 - 144 = 0
Так как дискриминант равен нулю то, квадратное уравнение имеет один действительных корень:
x = 122·4 = 1.5
3x2 - 4x - 1 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-4)2 - 4·3·(-1) = 16 + 12 = 28
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = 4 - √282·3 = 23 - 13√7 ≈ -0.21525043702153024
x2 = 4 + √282·3 = 23 + 13√7 ≈ 1.5485837703548635
2x2 - 9x + 15 = 0 Найдем дискриминант квадратного уравнения: D = b2 - 4ac = (-9)2 - 4·2·15 = 81 - 120 = -39 Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.